
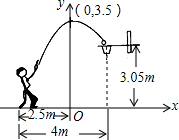
 宜昌四中男子籃球隊在2016全區籃球比賽中蟬聯冠軍,讓全校師生倍受鼓舞.在一次與第25中學的比賽中,運動員小濤在距籃下4米處跳起投籃,如圖所示,球運行的路線是拋物線,當球運行的水平距離為2.5米時,達到最大高度3.5米,然后準確落入籃圈.已知籃圈中心到地面的距離為3.05米.
宜昌四中男子籃球隊在2016全區籃球比賽中蟬聯冠軍,讓全校師生倍受鼓舞.在一次與第25中學的比賽中,運動員小濤在距籃下4米處跳起投籃,如圖所示,球運行的路線是拋物線,當球運行的水平距離為2.5米時,達到最大高度3.5米,然后準確落入籃圈.已知籃圈中心到地面的距離為3.05米.分析 (1)設拋物線的表達式為y=ax2+3.5,利用待定系數法,可得a的值.
(2)設球出手時,他跳離地面的高度為hm,則可得h+2.05=-0.2×(-2.5)2+3.5.
解答 解:(1)∵當球運行的水平距離為2.5米時,達到最大高度3.5米,
∴拋物線的頂點坐標為(0,3.5),
∴設拋物線的表達式為y=ax2+3.5.
由圖知圖象過以下點:(1.5,3.05).
∴2.25a+3.5=3.05,
解得:a=-0.2,
∴拋物線的表達式為y=-0.2x2+3.5.
(2)設球出手時,他跳離地面的高度為hm,
因為(1)中求得y=-0.2x2+3.5,
則球出手時,球的高度為h+1.8+0.25=(h+2.05)m,
∴h+2.05=-0.2×(-2.5)2+3.5,
∴h=0.2(m).
答:球出手時,他跳離地面的高度為0.2m.
點評 本題考查二次函數的應用、待定系數法確定函數解析式等知識,體現了數學建模的數學思想,難度不大,能夠結合題意利用二次函數不同的表達形式求得解析式是解答本題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
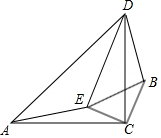 如圖,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,
如圖,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
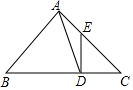 在△ABC中,∠BAC=90°,∠B=45°,D為BC上一點,BD=AB,DE⊥BC,交AC于點E.
在△ABC中,∠BAC=90°,∠B=45°,D為BC上一點,BD=AB,DE⊥BC,交AC于點E.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com