Question

6．（1）已知⊙O的直徑為6，圓心O到直線l的距離為5，
①直線l與⊙O的位置關系是相離；
②若點P為⊙O上一動點，求點P到直線l的距離的最大值和最小值．
（2）如圖，在⊙O中，直徑AB=10，弦CD⊥AB，垂足為E，BE=2，求弦CD的長．

Answer 1

分析 （1）①根據圓心距和兩圓半徑的之間關系可得出兩圓之間的位置關系；
②點P到直線l的距離的最大值=圓心O到直線l的距離+⊙O的半徑，最小值=圓心O到直線l的距離-⊙O的半徑；
（2）如圖，連接OC；首先證明CE=DE；其次運用勾股定理求出CE的長，即可解決問題．

解答 解：（1）①∵⊙O的直徑為6，
∴⊙O的半徑為3，
∵圓心O到直線l的距離是5，5＞3，
∴直線l與⊙O的位置關系是相離；
②點P到直線l的距離的最大值=5+6÷2=8，最小值=5-6÷2=2；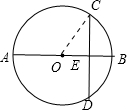
（2）如圖，連接OC；
∵直徑AB=10，BE=2，
∴OE=5-2=3，OC=5；
∵弦CD⊥AB，
∴CE=DE；
由勾股定理得：
CE=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴CD=2CE=8．
故答案為：相離．

點評 此題考查了由數量關系來判斷兩圓位置關系的方法．設兩圓的半徑分別為R和r，且R≥r，圓心距為P：外離P＞R+r；外切P=R+r；相交R-r＜P＜R+r；內切P=R-r；內含P＜R-r．考查了勾股定理、垂徑定理等幾何知識點及其應用問題；解題的關鍵是作輔助線，靈活運用勾股定理、垂徑定理等幾何知識點來分析、判斷、求解．