
分析 ①把p、q看作方程x2-2x-5=0的兩根,根據•根與系數的關系得到p+q=2,pq=-5;
②先把5q2+2q-1=0變形為($\frac{1}{q}$)2-2•$\frac{1}{q}$-5=0,則p、$\frac{1}{q}$可看作方程x2-2x-5=0的兩根,根據根與系數關系得到p+$\frac{1}{q}$=2,p•$\frac{1}{q}$=-5,再利用完全平方公式變形得${p^2}+\frac{1}{q^2}$=(p+$\frac{1}{q}$)2-2p•$\frac{1}{q}$,然后利用整體代入的方法計算.
解答 解:①∵p2-2p-5=0,q2-2q-5=0,p≠q,
∴p、q可看作方程x2-2x-5=0的兩根,
∴p+q=2,pq=-5;
故答案為2,-5;
②∵5q2+2q-1=0,
∴($\frac{1}{q}$)2-2•$\frac{1}{q}$-5=0,
而pq≠1,
∴p、$\frac{1}{q}$可看作方程x2-2x-5=0的兩根,
∴p+$\frac{1}{q}$=2,p•$\frac{1}{q}$=-5,
∴${p^2}+\frac{1}{q^2}$=(p+$\frac{1}{q}$)2-2p•$\frac{1}{q}$=22-2×(-5)=14.
點評 本題考查了根與系數的關系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的兩根時,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2460(1-x)2=1800 | B. | 1800(1+x)2=2460 | ||
| C. | 1800(1-x)2=2460 | D. | 1800+1800(1+x)+1800(1+x)2=2460 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 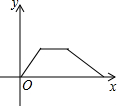 | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com