
 如圖,四邊形ABCD中,∠ABC=∠ADC=90°,E、F分別是AC、BD的中點(diǎn),∠BAC=15°,∠DAC=45°,則$\frac{EF}{CD}$的值為$\frac{\sqrt{2}}{4}$.
如圖,四邊形ABCD中,∠ABC=∠ADC=90°,E、F分別是AC、BD的中點(diǎn),∠BAC=15°,∠DAC=45°,則$\frac{EF}{CD}$的值為$\frac{\sqrt{2}}{4}$. 分析 連接BE,ED,根據(jù)∠ABC=∠ADC=90°且E為AC中點(diǎn),求證△BED是等腰三角形,再利用等腰三角形的高,中線,角平分線三線合一的性質(zhì)得到EF⊥BD,
根據(jù)圓周角定理得到∠DEF=60°,求得EF=$\frac{1}{2}$DE,CD=$\sqrt{2}$DE,于是得出結(jié)論.
解答 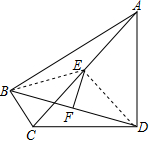 解:連接BE,ED,
解:連接BE,ED,
∵∠ABC=∠ADC=90°且E為AC中點(diǎn),
∴DE=$\frac{1}{2}$AC,BE=$\frac{1}{2}$AC,
∴BE=DE,
∵F為BD中點(diǎn),
∴EF⊥BD,
∵∠ABC=∠ADC=90°,
∴A,B,C,D四點(diǎn)共圓,
∵∠BAC=15°,∠DAC=45°,
∴∠BAD=60°,
∴∠BED=120°,
∴∠FED=60°,
∴EF=$\frac{1}{2}$DE,
∵CD=$\sqrt{2}$DE,
∴$\frac{EF}{CD}$=$\frac{\sqrt{2}}{4}$.
故答案為:$\frac{\sqrt{2}}{4}$.
點(diǎn)評 此題主要考查直角三角形斜邊上的中線等于斜邊的一半和等腰三角形的性質(zhì)等知識點(diǎn),解答此題的關(guān)鍵是連接BE,ED,根據(jù)∠ABC=∠ADC=90°且E為AC中點(diǎn),證出△BED是等腰三角形.


 名題金卷系列答案
名題金卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
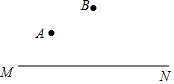 A、B兩廠在公路MN同側(cè),擬在公路邊建一貨場C,若由B廠獨(dú)家興建,并考慮B廠的利益,則要求貨場離B廠最近,請?jiān)趫D中作出此時(shí)貨場C的位置,并說出這樣做的道理.
A、B兩廠在公路MN同側(cè),擬在公路邊建一貨場C,若由B廠獨(dú)家興建,并考慮B廠的利益,則要求貨場離B廠最近,請?jiān)趫D中作出此時(shí)貨場C的位置,并說出這樣做的道理.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 1-$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$-1 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 二次函數(shù)y=ax2+bx+c的圖象如圖所示(a、b、c為常數(shù)),則函數(shù)y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐標(biāo)系中的圖象,可能是( )
二次函數(shù)y=ax2+bx+c的圖象如圖所示(a、b、c為常數(shù)),則函數(shù)y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐標(biāo)系中的圖象,可能是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3x+3y=6xy | B. | -y2-y2=0 | C. | 3(x+8)=3x+8 | D. | -(6x+2y)=-6x-2y |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com