
 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:初中數學 來源: 題型:選擇題
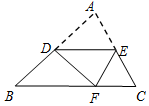 如圖,D是AB的中點,將△ABC沿過點D的直線折疊,使點A落在BC邊上點F處,若∠B=50°,則∠EDF的度數為( )
如圖,D是AB的中點,將△ABC沿過點D的直線折疊,使點A落在BC邊上點F處,若∠B=50°,則∠EDF的度數為( )| A. | 40° | B. | 50° | C. | 60° | D. | 80° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
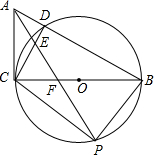 如圖,在△ABC中,∠ACB=90°,以直角邊BC為直徑的⊙O交AB于點D,連接CD,∠CAB的角平分線交CD于點E,交BC于點F,交⊙O于點P.
如圖,在△ABC中,∠ACB=90°,以直角邊BC為直徑的⊙O交AB于點D,連接CD,∠CAB的角平分線交CD于點E,交BC于點F,交⊙O于點P.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
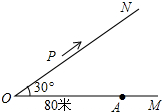 如圖,∠MON=30°,在距離O點80米的A處有一所學校,當重型運輸卡車P沿道路ON方向行駛時,距離卡車50米范圍內都會受到卡車噪聲的影響.
如圖,∠MON=30°,在距離O點80米的A處有一所學校,當重型運輸卡車P沿道路ON方向行駛時,距離卡車50米范圍內都會受到卡車噪聲的影響.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
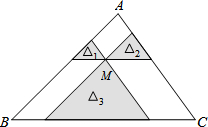 如圖,點M是△ABC內一點,過點M分別作直線平行于△ABC的各邊,所形成的三個小三角形△1,△2,△3(圖中陰影部分)的面積分別是4,9和16,則△ABC的面積是( )
如圖,點M是△ABC內一點,過點M分別作直線平行于△ABC的各邊,所形成的三個小三角形△1,△2,△3(圖中陰影部分)的面積分別是4,9和16,則△ABC的面積是( )| A. | 49 | B. | 64 | C. | 100 | D. | 81 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com