
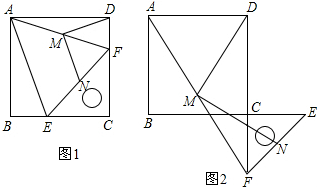
分析 (1)寫出結論1和2;
(2)結論1,根據三角形中位線得:MN=$\frac{1}{2}AE$,根據直角三角形斜邊中線得:DM=$\frac{1}{2}$AF,證明△ABE≌△ADF可以得出結論;
結論2:主要證明∠NMD=∠BAD=90°即可;
(3)連接AE,交MD于點G,標記出各個角,首先證明出MN∥AE,MN=$\frac{1}{2}$AE,再有(1)的結論以及角角之間的數量關系得到∠DMN=∠DGE=90°.
解答 解:(1)結論1:DM、MN的數量關系是:DM=MN,
結論2:DM、MN的位置關系是:DM⊥MN,
故答案為:DM=MN,DM⊥MN;
(2)結論1:DM=MN,理由是:
如圖1,∵M是AF的中點,N是EF的中點,
∴MN=$\frac{1}{2}$AE,
∵四邊形ABCD是正方形,
∴∠ADF=∠B=90°,AB=AD=BC=CD,
∴DM=$\frac{1}{2}$AF,
∵△ECF是等腰直角三角形,
∴EC=FC,
∴BE=DF,
在△ABE和△ADF中,
∵$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠ADF}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△ADF(SAS),
∴AE=AF,
∴DM=MN;
結論2,DM、MN的位置關系是:DM⊥MN,理由是:
如圖1,∵M是AF的中點,N是EF的中點,
∴MN∥AE,
∴∠NMF=∠EAF,
∵△ABE≌△ADF,
∴∠BAE=∠FAD,
Rt△ADF中,∵M是AF的中點,
∴AM=DM,
∴∠FAD=∠MDA,
∵∠FMD=∠FAD+∠MDA=∠FAD+∠BAE,
∴∠DMN=∠NMF+∠FMD=∠EAF+∠BAE+∠FAD=90°,
∴DM⊥MN;
(3)(2)中的兩個結論還成立,
證明:連接AE,交MD于點G,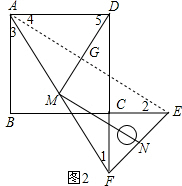
∵點M為AF的中點,點N為EF的中點,
∴MN∥AE,MN=$\frac{1}{2}$AE,
由(1)同理可證,
AB=AD=BC=CD,∠B=∠ADF,CE=CF,
又∵BC+CE=CD+CF,即BE=DF,
∴△ABE≌△ADF,
∴AE=AF,
在Rt△ADF中,
∵點M為AF的中點,
∴DM=$\frac{1}{2}$AF,
∴DM=MN,
∵△ABE≌△ADF,
∴∠1=∠2,
∵AB∥DF,
∴∠1=∠3,
同理可證:∠2=∠4,
∴∠3=∠4,
∵DM=AM,
∴∠MAD=∠5,
∴∠DGE=∠5+∠4=∠MAD+∠3=90°,
∵MN∥AE,
∴∠DMN=∠DGE=90°,
∴DM⊥MN.
點評 本題主要考查正方形的性質以及全等三角形的判定與性質等知識點,解答本題的關鍵是利用好各小題之間的聯系,此題難度不大,但是角與角之間的數量關系有點復雜,請同學們解答的時候注意.


 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案科目:初中數學 來源: 題型:解答題
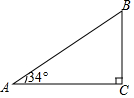 如圖,某山坡坡長AB為110米,坡角(∠A)為34°,求坡高BC及坡寬AC.(結果精確到0.1米)
如圖,某山坡坡長AB為110米,坡角(∠A)為34°,求坡高BC及坡寬AC.(結果精確到0.1米)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
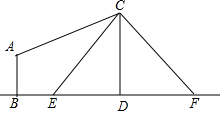 如圖,電線桿CD上的C處引拉線CE,CF固定電線桿,在離電線桿6米的B處安置測角儀(點B,E,D在同一直線上),在A處測得電線桿上C處的仰角為30°,已知測角儀的高AB=$\sqrt{3}$米,BE=3米,求拉線CE的長.
如圖,電線桿CD上的C處引拉線CE,CF固定電線桿,在離電線桿6米的B處安置測角儀(點B,E,D在同一直線上),在A處測得電線桿上C處的仰角為30°,已知測角儀的高AB=$\sqrt{3}$米,BE=3米,求拉線CE的長.查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com