

分析 (1)根據正比例函數與反比例函數的圖象的交點關于原點對稱,即可解決問題,利用圖象根據正比例函數的圖象在反比例函數的圖象的上方,即可確定自變量x的范圍.
(2)①利用對角線互相平分的四邊形是平行四邊形證明即可.
②利用分割法求面積即可.
(3)根據矩形的性質、正方形的性質即可判定.
解答 解:(1)∵A、B關于原點對稱,A(3,1),
∴點B的坐標為(-3,-1).
由圖象可知,當-3≤x<0或x≥3時,$\frac{k}{x}$≤k′x.
故答案為(-3,-1),-3≤x<0或x≥3
(2)①∵A、B關于原點對稱,P、Q關于原點對稱,
∴OA=OB,OP=OQ,
∴四邊形APBQ是平行四邊形.
故答案為:平行四邊形;
②∵點A的坐標為(3,1),
∴k=3×1=3,
∴反比例函數的解析式為y=$\frac{3}{x}$,
∵點P的橫坐標為1,
∴點P的縱坐標為3,
∴點P的坐標為(1,3),
由雙曲線關于原點對稱可知,點Q的坐標為(-1,-3),點B的坐標為(-3,-1),
如圖2,過點A、B分別作y軸的平行線,過點P、Q分別作x軸的平行線,分別交于C、D、E、F,
則四邊形CDEF是矩形,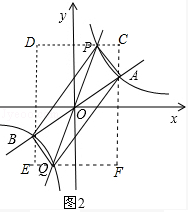
CD=6,DE=6,DB=DP=4,CP=CA=2,
則四邊形APBQ的面積=矩形CDEF的面積-△ACP的面積-△PDB的面積-△BEQ的面積-△AFQ的面積
=36-2-8-2-8
=16.
(3)mn=k時,四邊形APBQ是矩形,
不可能是正方形.
理由:當AB⊥PQ時四邊形APBQ是正方形,此時點A、P在坐標軸上,由于點A,P可能達到坐標軸故不可能是正方形,即∠POA≠90°.
因為mn=k,易知P、A關于直線y=x對稱,所以PO=OA=OB=OQ,所以四邊形APBQ是矩形.
點評 本題考查反比例函數綜合題、平行四邊形的判定和性質、矩形的判定和性質,四邊形的面積等知識,解題的關鍵是學會利用對稱的性質解決問題,學會用分割法求面積,學會利用圖象確定自變量的取值范圍,屬于中考壓軸題.


 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:初中數學 來源: 題型:解答題
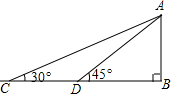 如圖,某數學興趣小組為測得校園里旗桿AB的高度,在操場的平地上選擇一點C,測得旗桿頂端點A的仰角為30°,再向旗桿的方向前進12米,到達點D處(C,D,B三點在同一直線上),又測得旗桿頂端點A的仰角為45°,請計算旗桿AB的高度.(結果保留根號)
如圖,某數學興趣小組為測得校園里旗桿AB的高度,在操場的平地上選擇一點C,測得旗桿頂端點A的仰角為30°,再向旗桿的方向前進12米,到達點D處(C,D,B三點在同一直線上),又測得旗桿頂端點A的仰角為45°,請計算旗桿AB的高度.(結果保留根號)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
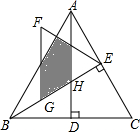 如圖,△ABC是等邊三角形,高AD、BE相交于點H,BC=4,在BE上截取BG=2,以GE為邊作等邊三角形GEF,則△ABH與△GEF重疊(陰影)部分的面積為$\frac{\sqrt{3}}{6}$.
如圖,△ABC是等邊三角形,高AD、BE相交于點H,BC=4,在BE上截取BG=2,以GE為邊作等邊三角形GEF,則△ABH與△GEF重疊(陰影)部分的面積為$\frac{\sqrt{3}}{6}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com