
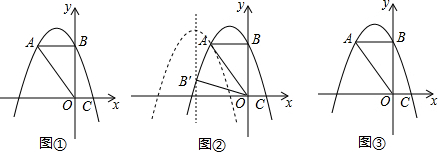
分析 (1)如圖①,利用AB⊥y軸得到B(0,3),然后把B點坐標代入拋物線解析式可求出c的值;
(2)如圖②,設B′(a,b),利用折疊的性質得AB′=AB=2,OB′=OB=3,根據兩點間的距離公式得到$\left\{\begin{array}{l}{(a+2)^{2}+(b-3)^{2}={2}^{2}}\\{{a}^{2}+{b}^{2}={3}^{2}}\end{array}\right.$,則解方程組可得到B′(-$\frac{36}{13}$,$\frac{15}{13}$),于是可確定P;
(3)如圖③,先確定C(1,0),由于BC只能為邊,不能為對角線,則應用EF∥BC,EF=BC可得到F點的縱坐標為3或-3,當y=3時,-x2-2x+3=3,解方程確定此時F點的坐標為(-2,3),利用平行四邊形的性質可得到對應E點坐標為(-1,0);當y=-3時,-x2-2x+3=-3,解得方程得到F點的坐標為(-1+$\sqrt{7}$,-3)或(-1-$\sqrt{7}$,-3),利用平行四邊形的性質可確定對應的E點的坐標(-2+$\sqrt{7}$,0)或(-2-$\sqrt{7}$,0).
解答 解:(1)如圖①,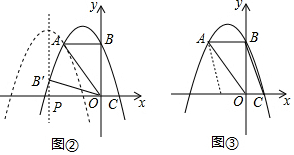
∵點A的坐標是(-2,3),點A作AB⊥y軸,
∴B(0,3),
把B(0,3)代入y=-x2-2x+c得c=3;
(2)如圖②,設B′(a,b),
∵△OAB沿直線OA翻折,記點B的對應點為B′,
∴AB′=AB=2,OB′=OB=3,
∴$\left\{\begin{array}{l}{(a+2)^{2}+(b-3)^{2}={2}^{2}}\\{{a}^{2}+{b}^{2}={3}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=0}\\{b=3}\end{array}\right.$或$\left\{\begin{array}{l}{a=-\frac{36}{13}}\\{b=\frac{15}{13}}\end{array}\right.$,
∴B′(-$\frac{36}{13}$,$\frac{15}{13}$),
∵點B'恰好落在平移后隨物線的對稱軸上,
∴P(-$\frac{36}{13}$,0);
(3)如圖③,拋物線解析式為y=-x2-2x+3,當y=0時,-x2-2x+3=0,解得x1=1,x2=-3,則C(1,0),
以點B、C、E、F為頂點的四邊形是平行四邊形,則BC為邊,不能為對角線,
∴EF∥BC,EF=BC,
∴F點的縱坐標為3或-3,
當y=3時,-x2-2x+3=3,解得x1=0,x2=-2,此時F點的坐標為(-2,3),所以E點坐標為(-1,0),
當y=-3時,-x2-2x+3=-3,解得x1=-1+$\sqrt{7}$,x2=-1-$\sqrt{7}$,
此時F點的坐標為(-1+$\sqrt{7}$,-3)或(-1-$\sqrt{7}$,-3),對應的E點的坐標(-2+$\sqrt{7}$,0)或(-2-$\sqrt{7}$,0),
綜上所述,E點的坐標為(-1,0),(-2+$\sqrt{7}$,0)或(-2-$\sqrt{7}$,0).
點評 本題考查了二次函數的綜合題:熟練掌握二次函數圖象上點的坐標特征、二次函數的性質、折疊的性質和平行四邊形的性質;會運用待定系數法求拋物線的解析式;能運用兩點間的距離公式計算線段的長;會應用分類討論的思想解決數學問題.


科目:初中數學 來源: 題型:解答題
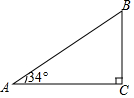 如圖,某山坡坡長AB為110米,坡角(∠A)為34°,求坡高BC及坡寬AC.(結果精確到0.1米)
如圖,某山坡坡長AB為110米,坡角(∠A)為34°,求坡高BC及坡寬AC.(結果精確到0.1米)查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
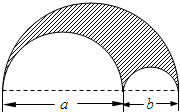 如圖,一塊直徑為a+b的半圓形鋼板,從中挖去直徑分別為a與b的兩個半圓
如圖,一塊直徑為a+b的半圓形鋼板,從中挖去直徑分別為a與b的兩個半圓查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com