
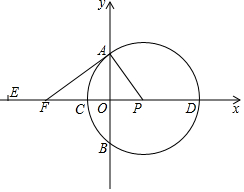
 如圖,平面直角坐標系中,點P(6,0),以P為圓心,10為半徑的圓分別交坐標軸于點A、B、C、D.
如圖,平面直角坐標系中,點P(6,0),以P為圓心,10為半徑的圓分別交坐標軸于點A、B、C、D.分析 (1)先確定出OP=6,根據勾股定理求出OA=8,即可得出點A的坐標;
(2)先確定出點D的坐標,利用對稱點的性質確定出點E的坐標,即可確定出n的值,從而得出點F的坐標,最后用兩點間的距離公式求出AF的長.
解答 解:(1)∵點P(6,0),
∴OP=6,∵⊙P的半徑為10,
∴AP=PD=10,
在Rt△AOP中,AP=10,OP=6,
∴OA=$\sqrt{A{P}^{2}-O{P}^{2}}$=8,
∴A(0,8);
(2)∵⊙P的半徑為10,
∴AP=PD=10,
∵OP=6,
∴OD=OP+PD=16,
∴D(16,0),
∵點D關于y軸的對稱點是E(n,0),
∴n=-16,
∵點F(n+1,0),
∴F(-15,0),
∵A(0,8),
∴AF=$\sqrt{1{5}^{2}+{8}^{2}}$=17,
∴線段AF的長為17.
點評 此題要考查了垂定定理,勾股定理,對稱的性質,兩點間的距離公式,解(1)的關鍵是根據勾股定理求出OA,解(2)的關鍵是確定出n的值,是一道基礎題.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:選擇題
 如圖,將三個同樣的正方形的一個頂點重合放置,如果∠1=45°,∠3=30°時,那么∠2的度數是( )
如圖,將三個同樣的正方形的一個頂點重合放置,如果∠1=45°,∠3=30°時,那么∠2的度數是( )| A. | 15° | B. | 25° | C. | 30° | D. | 45° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
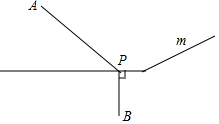 如圖所示,在兩個村莊A,B附近的河流可以近似地看成一條折線段(圖中m)A,B分別在河的兩旁,現要在河邊修一個水泵站,同時向A,B兩村供水,為了節約建設的費用,就要使所鋪設的管道最短,某人甲提出了這樣的建議:從點B向河道作垂線交m于點P,則點P為水泵站的位置.
如圖所示,在兩個村莊A,B附近的河流可以近似地看成一條折線段(圖中m)A,B分別在河的兩旁,現要在河邊修一個水泵站,同時向A,B兩村供水,為了節約建設的費用,就要使所鋪設的管道最短,某人甲提出了這樣的建議:從點B向河道作垂線交m于點P,則點P為水泵站的位置.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,矩形OABC的兩邊OA,OC分別在x軸、y軸的正半軸上,OA=4,OC=2,點P從點O出發,沿x軸以每秒1個單位的速度向點A勻速運動,到達點A時停止運動,設點P運動的時間是t秒(t>0),過點P作∠DPA=∠CPO,且PD=$\frac{1}{2}$CP,連接DA.
如圖,在平面直角坐標系中,矩形OABC的兩邊OA,OC分別在x軸、y軸的正半軸上,OA=4,OC=2,點P從點O出發,沿x軸以每秒1個單位的速度向點A勻速運動,到達點A時停止運動,設點P運動的時間是t秒(t>0),過點P作∠DPA=∠CPO,且PD=$\frac{1}{2}$CP,連接DA.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
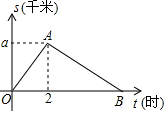 平頂山市教育局舉行'重走長征路”健步活動,某教師從起點體育村沿建設路到市生態園.再沿原路返回.該教師離開起點的路程S(千米)與步行時間t(小時)之間的函數關系如圖所示.其中從起點到市生態園的平均速度是4千米/小時.用2小時.根據圖象提供信息.解答下列問題
平頂山市教育局舉行'重走長征路”健步活動,某教師從起點體育村沿建設路到市生態園.再沿原路返回.該教師離開起點的路程S(千米)與步行時間t(小時)之間的函數關系如圖所示.其中從起點到市生態園的平均速度是4千米/小時.用2小時.根據圖象提供信息.解答下列問題查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com