
分析 首先把括號內的分式通分相加,把除法轉化為乘法,計算乘法即可化簡,然后化簡x的值,代入求解即可.
解答 解:原式=[$\frac{2-2x}{x+1}$+x-1]÷$\frac{x(x-1)}{x+1}$
=$\frac{2-2x+{x}^{2}-1}{x+1}$•$\frac{x+1}{x(x-1)}$
=$\frac{{x}^{2}-2x+1}{x(x-1)}$
=$\frac{(x-1)^{2}}{x(x-1)}$
=$\frac{x-1}{x}$.
當x=tan30°=$\frac{\sqrt{3}}{3}$時,原式=$\frac{\frac{\sqrt{3}}{3}-1}{\frac{\sqrt{3}}{3}}$=1-$\sqrt{3}$.
點評 本題考查了分式的化簡求值,正確對所求的分式進行通分、約分是關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖△PAB中,PA=PB,PB為⊙O的切線,B為切點,連接OP交AB于點C,延長BO與⊙O交于點D、與PA的延長線交于點E
如圖△PAB中,PA=PB,PB為⊙O的切線,B為切點,連接OP交AB于點C,延長BO與⊙O交于點D、與PA的延長線交于點E查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,是某副食品公司銷售糖果的總利潤y(元)與銷售量x(千克)之間的函數圖象(總利潤=總銷售額-總成本),該公司想通過“不改變總成本,提高糖果售價”的方案解決銷售不佳的現狀,下面給出的四個圖象,虛線均表示新的銷售方案中總利潤與銷售量之間的函數圖象,則能反映該公司改進方案的是( )
如圖,是某副食品公司銷售糖果的總利潤y(元)與銷售量x(千克)之間的函數圖象(總利潤=總銷售額-總成本),該公司想通過“不改變總成本,提高糖果售價”的方案解決銷售不佳的現狀,下面給出的四個圖象,虛線均表示新的銷售方案中總利潤與銷售量之間的函數圖象,則能反映該公司改進方案的是( )| A. | 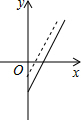 | B. | 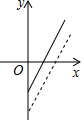 | C. | 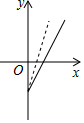 | D. | 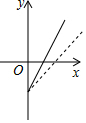 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
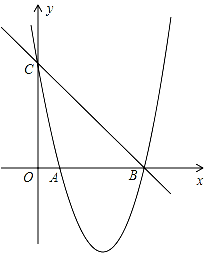 如圖,已知拋物線y=x2+bx+c的圖象與x軸的一個交點為B(5,0),另一個交點為A,且與y軸交于點C(0,5).
如圖,已知拋物線y=x2+bx+c的圖象與x軸的一個交點為B(5,0),另一個交點為A,且與y軸交于點C(0,5).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 若將直尺的0cm刻度線與半徑為5cm的量角器的0°線對齊,并讓量角器沿直尺的邊緣無滑動地滾動,則直尺上的10cm刻度線對應量角器上的度數約為115°.(保留π)
若將直尺的0cm刻度線與半徑為5cm的量角器的0°線對齊,并讓量角器沿直尺的邊緣無滑動地滾動,則直尺上的10cm刻度線對應量角器上的度數約為115°.(保留π)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com