Question

19．已知：關于x的一元二次方程ax²-2（a-1）x+a-2=0（a＞0）．
（1）求證：方程有兩個不相等的實數根；
（2）設方程的兩個實數根分別為x₁，x₂（其中x₁＞x₂）．若y是關于a的函數，且y=ax₂•x₁，求這個函數的表達式；
（3）將（2）中所得的函數的圖象在直線a=2的左側部分沿直線a=2翻折，圖象的其余部分保持不變，得到一個新的圖象．請你結合這個新的圖象直接寫出：當關于a的函數y=2a+b的圖象與此圖象有兩個公共點時，b的取值范圍是-11＜b＜-5．

Answer 1

分析 （1）根據一元二次方程的根的判別式判斷即可；
（2）先根據一元二次方程的求根公式得出x₁，x₂，即可得出函數函數關系式；
（3）畫出新函數的圖形和直線y=2a+b，利用圖形和直線與y軸的交點坐標即可得出結論．

解答 （1）證明：∵ax²-2（a-1）x+a-2=0（a＞0）是關于x的一元二次方程，
∴△=[-2（a-1）]²-4a（a-2）=4＞0，
∴方程ax²-2（a-1）x+a-2=0（a＞0）有兩個不相等的實數根．


（2）解：由求根公式，得x=$\frac{2（a-1）±\sqrt{△}}{2a}$=$\frac{2（a-1）±2}{2a}$．
∴x=1或x=1-$\frac{2}{a}$．   
∵a＞0，x₁＞x₂，
∴x₁=1，x₂=1-$\frac{2}{a}$，
∴y=ax₂•x₁=a×（1-$\frac{2}{a}$）•1=a-2．
即函數的表達式y=a-2（a＞0），


（3）解：如圖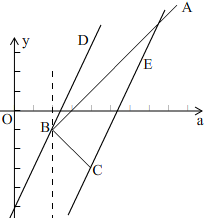，直線BD剛好和折線CBA只有一個公共點，再向下平移，就和這些CBA有兩個公共點，
繼續向下平移到直線CE的位置和直線CBA剛好有1個公共點，再向下平移和這些CBA也只有一個公共點，
由（2）知，函數的表達式y=a-3（a＞0），
當a=2時，y=2-3=-1，
∴B（2，-1），
由折疊得，C（4，-3），
當函數y=2a+b的圖象過點B時，
∴-1=2×2+b，
∴b=-5，
當函數y=2a+b的圖象過點C時，
∴-3=2×4+b，
∴b=-11，
∴-11＜b＜-5．
故答案為：-11＜b＜-5．

點評 此題是翻折變換，主要考查了一元二次方程的根的判別式，求根公式，一次函數的性質，函數圖象的畫法，解本題的關鍵是求出函數的表達式y=a-3（a＞0），畫出函數圖象是解本題的難點，注意b的范圍兩個端點都不能取，此題（3）可以通過函數關系式求出射線BA的解析式，線段BC的解析式，再利用直線y=2a+b既和射線BA有交點，也和線段BC有交點，即可求出b的范圍．