

分析 (1)如圖1中,將△ABE繞點B順時針旋轉90°得△CBE′,連接EE′.只要證明CE′2+EC2=EE′2,推出∠ECE′=90°,推出∠ECB+∠BCE′=∠ECB+∠BAE=90°,即A、E、C共線,推出點E在正方形ABCD的對角線上.
(2)如圖2中,將△ABE繞點B逆時針旋轉60°得△A′BE′,連結A′C,作A′H⊥BC于H.首先證明△EBE′為等邊三角形,推出EE′=BE,A′E′=AE,BA′=BA,∠ABA′=60°,因為A′E′+E′E+EC≥A′C,所以AE+BE+CE≥AC(當且僅當點E′、點E在AC上時,取等號),AE+BE+CE有最小值,最小值為A′C的長,設正方形的邊長為a,在Rt△A′BH中,∠A′BH=30°,A′H=$\frac{1}{2}$A′B=$\frac{1}{2}$a,BH=$\sqrt{3}$A′H=$\frac{\sqrt{3}}{2}$a,CH=a+$\frac{\sqrt{3}}{2}$a,在Rt△A′CH中,根據A′C2=A′H2+CH2,列出方程即可解決問題.
解答 (1)證明:如圖1中,將△ABE繞點B順時針旋轉90°得△CBE′,連接EE′.
∵BE=BE′,∠EBE′=90°,AE=CE′,
∴EE′=$\sqrt{2}$BE,
∵EA2+EC2=2EB2,
∴CE′2+EC2=EE′2,
∴∠ECE′=90°,
∴∠ECB+∠BCE′=∠ECB+∠BAE=90°,
∴A、E、C共線,
∴點E在正方形ABCD的對角線上.
(2)解:如圖2中,將△ABE繞點B逆時針旋轉60°得△A′BE′,連結A′C,作A′H⊥BC于H.
∵△ABE繞點B逆時針旋轉60°得△A′BE′,
∴BE=BE′,∠EBE′=60°,
∴△EBE′為等邊三角形,
∴EE′=BE,
∴A′E′=AE,BA′=BA=2,∠ABA′=60°,
∵A′E′+E′E+EC≥A′C,
∴AE+BE+CE≥AC(當且僅當點E′、點E在AC上時,取等號),
∴AE+BE+CE有最小值,最小值為A′C的長,設正方形的邊長為a,
在Rt△A′BH中,∠A′BH=30°,
∴A′H=$\frac{1}{2}$A′B=$\frac{1}{2}$a,BH=$\sqrt{3}$A′H=$\frac{\sqrt{3}}{2}$a,
∴CH=a+$\frac{\sqrt{3}}{2}$a,
在Rt△A′CH中,A′C2=A′H2+CH2,
∴($\frac{1}{2}$a)2+(a+$\frac{\sqrt{3}}{2}$a)2=($\sqrt{6}$+$\sqrt{2}$)2,
解得a=2.
∴正方形的邊長為2.
點評 本題正方形的性質、最短問題、旋轉變換、勾股定理以及勾股定理的逆定理等知識,解題的關鍵是學會利用旋轉變換添加輔助線,構造全等三角形,學會利用兩點之間線段最短解決最短問題,所以中考常考題型.


科目:初中數學 來源: 題型:解答題
 已知:關于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).
已知:關于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 三邊a、b、c | m | l×m | S |
| 3、4、5 | 2 | 24 | 6 |
| 5、12、13 | 4 | 120 | 30 |
| 8、15、17 | 6 | 240 | 60 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
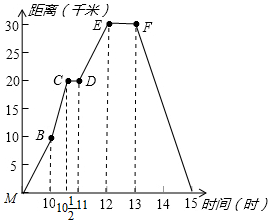 如圖所示,折線表示小麗騎車離家的距離與時間的關系,小麗上午九時離開家,下午十五時到家,根據折線圖所提供的信息,思考并回答下列問題:
如圖所示,折線表示小麗騎車離家的距離與時間的關系,小麗上午九時離開家,下午十五時到家,根據折線圖所提供的信息,思考并回答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
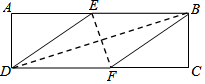 在矩形ABCD中,有一個菱形BFDE(點E,F分別在線段AB,CD上),記它們的面積分別為SABCD和SBFDE,現給出下列命題:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,則tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,則DF=2AD,則( )
在矩形ABCD中,有一個菱形BFDE(點E,F分別在線段AB,CD上),記它們的面積分別為SABCD和SBFDE,現給出下列命題:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,則tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,則DF=2AD,則( )| A. | ①是假命題,②是假命題 | B. | ①是真命題,②是假命題 | ||
| C. | ①是假命題,②是真命題 | D. | ①是真命題,②是真命題 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com