
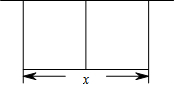
 某農場擬建兩間矩形種牛飼養室,飼養室的一面靠現有墻(墻長>50m),中間用一道墻隔開(如圖),己知計劃中的建筑材料可建圍墻的總長為50m,設兩飼養室合計長x(m),總占地面積為y(m2)
某農場擬建兩間矩形種牛飼養室,飼養室的一面靠現有墻(墻長>50m),中間用一道墻隔開(如圖),己知計劃中的建筑材料可建圍墻的總長為50m,設兩飼養室合計長x(m),總占地面積為y(m2)分析 (1)根據題意用含x的代數式表示出飼養室的寬,由矩形的面積=長×寬計算即可;
(2)由(1)可知y是x的二次函數,根據二次函數的性質分析即可.
解答 解:(1)∵圍墻的總長為50米,2間飼養室合計長x米,
∴飼養室的寬=$\frac{50-x}{3}$米,
∴總占地面積為y=x•$\frac{50-x}{3}$=-$\frac{1}{3}$x2+$\frac{50}{3}$x,(0<x<50);
(2)當兩間飼養室占地總面積達到200平方米時,則-$\frac{1}{3}$x2+$\frac{50}{3}$x=200,
解得:x=20或30;
答:各道墻長分別為20米、10米或30米、10米;
當占地面積達到210平方米時,則-$\frac{1}{3}$x2+$\frac{50}{3}$x=210,
方程的△<0,所以此方程無解,
所以占地面積不可能達到210平方米;
點評 此題主要考查了由實際問題列二次函數故選以及二次函數的最值問題和一元二次方程的應用,同時也利用了矩形的性質,解題時首先正確了解題意,然后根據題意列出方程即可解決問題.


科目:初中數學 來源: 題型:解答題
 如圖,若AB是CD的垂直平分線,E,F是AC,AD的中點,連結BE,BF.
如圖,若AB是CD的垂直平分線,E,F是AC,AD的中點,連結BE,BF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
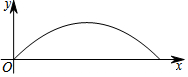 某校足球隊在一次訓練中,一球員從高2.4米的球門正前方m米處將球射向球門,球射向球門的路線呈拋物線,當球飛行的水平距離為6米時,球達到最高點,此時球離地面3米,建立如圖所示的平面直角坐標系
某校足球隊在一次訓練中,一球員從高2.4米的球門正前方m米處將球射向球門,球射向球門的路線呈拋物線,當球飛行的水平距離為6米時,球達到最高點,此時球離地面3米,建立如圖所示的平面直角坐標系查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,己知△ABC
如圖,己知△ABC查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
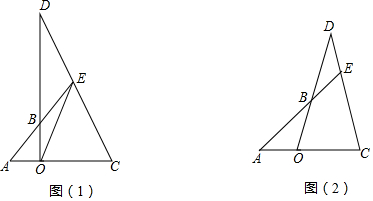
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com