
 如圖,若AB是CD的垂直平分線,E,F是AC,AD的中點,連結BE,BF.
如圖,若AB是CD的垂直平分線,E,F是AC,AD的中點,連結BE,BF.分析 (1)根據線段垂直平分線的性質解答;
(2)證明△ACB≌△ADB,根據全等三角形的性質證明結論.
解答 解:(1)∵AB是CD的垂直平分線,
∴AC=AD,BC=BD,
故答案為:AC=AD;BC=BD;
(2)∵AC=AD,E,F是AC,AD的中點,
∴AE=AF,
∵AC=AD,AB⊥CD,
∴∠CAB=∠DAB,
在△ACB和△ADB中,
$\left\{\begin{array}{l}{AE=AF}\\{∠EAB=∠DAB}\\{AB=AB}\end{array}\right.$,
∴△ACB≌△ADB,
∴BE=BF.
點評 本題考查的是線段垂直平分線的性質、全等三角形的判定和性質,掌握線段的垂直平分線上的點到線段的兩個端點的距離相等是解題的關鍵.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:初中數學 來源: 題型:選擇題
| x | 1 | 2 | 3 |
| 代數式的值 | -2 | -5 | -8 |
| A. | x-3 | B. | 2x-10 | C. | 3x-17 | D. | -3x+1 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖放置的△OAB1,△B1A1B2,△B2A2B3,…都是邊長為1的等邊三角形,點A在x軸上,點O,B1,B2,B3,…都在直線l上,則點A2的坐標是(2,$\sqrt{3}$),點A2017的坐標是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).
如圖放置的△OAB1,△B1A1B2,△B2A2B3,…都是邊長為1的等邊三角形,點A在x軸上,點O,B1,B2,B3,…都在直線l上,則點A2的坐標是(2,$\sqrt{3}$),點A2017的坐標是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在⊙O中,半徑OA⊥OB,過OA的中點C作FD∥OB交⊙O于D、F兩點,且DF=2$\sqrt{3}$,以O為圓心,OC為半徑作弧CE,交OB于點E.
如圖,在⊙O中,半徑OA⊥OB,過OA的中點C作FD∥OB交⊙O于D、F兩點,且DF=2$\sqrt{3}$,以O為圓心,OC為半徑作弧CE,交OB于點E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,一塊矩形綠地ABCD由籬笆圍著,并且由一條與AB邊平行的籬笆EF分開,已知AB=xm,籬笆的總長為600m.
如圖,一塊矩形綠地ABCD由籬笆圍著,并且由一條與AB邊平行的籬笆EF分開,已知AB=xm,籬笆的總長為600m.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
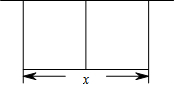 某農場擬建兩間矩形種牛飼養室,飼養室的一面靠現有墻(墻長>50m),中間用一道墻隔開(如圖),己知計劃中的建筑材料可建圍墻的總長為50m,設兩飼養室合計長x(m),總占地面積為y(m2)
某農場擬建兩間矩形種牛飼養室,飼養室的一面靠現有墻(墻長>50m),中間用一道墻隔開(如圖),己知計劃中的建筑材料可建圍墻的總長為50m,設兩飼養室合計長x(m),總占地面積為y(m2)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com