
 如圖,一塊矩形綠地ABCD由籬笆圍著,并且由一條與AB邊平行的籬笆EF分開,已知AB=xm,籬笆的總長為600m.
如圖,一塊矩形綠地ABCD由籬笆圍著,并且由一條與AB邊平行的籬笆EF分開,已知AB=xm,籬笆的總長為600m.分析 (1)根據題意可以用相應的代數式表示出矩形綠地的面積;
(2)將(1)中的解析式化為頂點式,即可解答本題.
解答 解:(1)由題意可得,
S=x•$\frac{600-3x}{2}$=$-\frac{3}{2}{x}^{2}+300x$,
即S=$-\frac{3}{2}{x}^{2}+300x$;
(2)∵S=$-\frac{3}{2}{x}^{2}+300x$=$-\frac{3}{2}(x-100)^{2}+15000$,
∴當x=100時,S取得最大值,此時,S=15000,
即矩形綠地的最大面積是15000m2.
點評 本題考查二次函數的應用,解答本題的關鍵是明確題意,列出相應的函數關系式,利用二次函數的頂點式求函數的最值.


科目:初中數學 來源: 題型:解答題
 如圖,若AB是CD的垂直平分線,E,F是AC,AD的中點,連結BE,BF.
如圖,若AB是CD的垂直平分線,E,F是AC,AD的中點,連結BE,BF.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
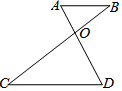 如圖,己知$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$,△AOB的面積是100 cm2,則△DOC的面積為( )
如圖,己知$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$,△AOB的面積是100 cm2,則△DOC的面積為( )| A. | 200 cm2 | B. | 300 cm2 | C. | 400 cm2 | D. | 500 cm2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2x-1 | B. | 2x+1 | C. | $\frac{1}{2}({x-1})$ | D. | $\frac{1}{2}({x+1})$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
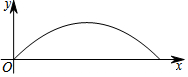 某校足球隊在一次訓練中,一球員從高2.4米的球門正前方m米處將球射向球門,球射向球門的路線呈拋物線,當球飛行的水平距離為6米時,球達到最高點,此時球離地面3米,建立如圖所示的平面直角坐標系
某校足球隊在一次訓練中,一球員從高2.4米的球門正前方m米處將球射向球門,球射向球門的路線呈拋物線,當球飛行的水平距離為6米時,球達到最高點,此時球離地面3米,建立如圖所示的平面直角坐標系查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com