

分析 (1)作EH⊥BC于H,根據(jù)矩形的判斷和性質(zhì)得到EH=CD=3,根據(jù)題意求出FH,根據(jù)勾股定理計(jì)算即可;
(2)根據(jù)矩形的性質(zhì)得到∠NFC=90°,NF=AB=3,根據(jù)翻轉(zhuǎn)變換的性質(zhì)得到NF=NE,根據(jù)題意列式計(jì)算即可.
解答 解:(1)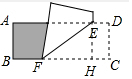 作EH⊥BC于H,
作EH⊥BC于H,
則四邊形DEHC是矩形,
∴EH=CD=3,
當(dāng)t=1時(shí),HC=DE=1,BF=2,
則FH=7-2-1=4,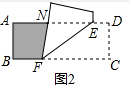
由勾股定理得,EF=$\sqrt{F{H}^{2}+E{H}^{2}}$=5;
(2)如圖2,當(dāng)ABFN是矩形時(shí),∠NFC=90°,NF=AB=3,
由折疊的性質(zhì)可知,∠NFE=∠CFE=45°,
∴NF=NE,即7-t-2t=3,
解得,t=$\frac{4}{3}$,
則當(dāng)t=$\frac{4}{3}$時(shí),矩形ABCD左邊無重疊部分為矩形.
點(diǎn)評(píng) 本題考查的是翻轉(zhuǎn)變換的性質(zhì)、矩形的性質(zhì),翻轉(zhuǎn)變換是一種對(duì)稱變換,它屬于軸對(duì)稱,折疊前后圖形的形狀和大小不變,位置變化,對(duì)應(yīng)邊和對(duì)應(yīng)角相等.


 黃岡冠軍課課練系列答案
黃岡冠軍課課練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,一塊矩形綠地ABCD由籬笆圍著,并且由一條與AB邊平行的籬笆EF分開,已知AB=xm,籬笆的總長(zhǎng)為600m.
如圖,一塊矩形綠地ABCD由籬笆圍著,并且由一條與AB邊平行的籬笆EF分開,已知AB=xm,籬笆的總長(zhǎng)為600m.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
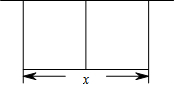 某農(nóng)場(chǎng)擬建兩間矩形種牛飼養(yǎng)室,飼養(yǎng)室的一面靠現(xiàn)有墻(墻長(zhǎng)>50m),中間用一道墻隔開(如圖),己知計(jì)劃中的建筑材料可建圍墻的總長(zhǎng)為50m,設(shè)兩飼養(yǎng)室合計(jì)長(zhǎng)x(m),總占地面積為y(m2)
某農(nóng)場(chǎng)擬建兩間矩形種牛飼養(yǎng)室,飼養(yǎng)室的一面靠現(xiàn)有墻(墻長(zhǎng)>50m),中間用一道墻隔開(如圖),己知計(jì)劃中的建筑材料可建圍墻的總長(zhǎng)為50m,設(shè)兩飼養(yǎng)室合計(jì)長(zhǎng)x(m),總占地面積為y(m2)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | y隨x的增大而增大 | B. | 圖象經(jīng)過點(diǎn)(3,-1) | ||
| C. | 圖象不經(jīng)過第二象限 | D. | 圖象與函數(shù)y=-x圖象有一個(gè)交點(diǎn) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
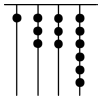 我國(guó)古代《易經(jīng)》一書中記載,遠(yuǎn)古時(shí)期,人們通過在繩子上打結(jié)來記錄數(shù)量,即“結(jié)繩計(jì)數(shù)”.如圖,一位母親在從右到左依次排列的繩子上打結(jié),滿七進(jìn)一,用來記錄孩子自出生后的天數(shù),由圖可知,孩子自出生后的天數(shù)是( )
我國(guó)古代《易經(jīng)》一書中記載,遠(yuǎn)古時(shí)期,人們通過在繩子上打結(jié)來記錄數(shù)量,即“結(jié)繩計(jì)數(shù)”.如圖,一位母親在從右到左依次排列的繩子上打結(jié),滿七進(jìn)一,用來記錄孩子自出生后的天數(shù),由圖可知,孩子自出生后的天數(shù)是( )| A. | 517 | B. | 84 | C. | 336 | D. | 1326 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 面積為8的正方形邊長(zhǎng)是$\sqrt{8}$ | B. | $\sqrt{8}$是無理數(shù) | ||
| C. | 在數(shù)軸上沒有對(duì)應(yīng)$\sqrt{8}$的點(diǎn) | D. | $\sqrt{8}$介于整數(shù)2和3之間 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
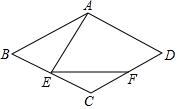 如圖,四邊形ABCD為菱形,∠C=120°,點(diǎn)E是BC上一點(diǎn).∠AEF=60°,EF交CD于F,求證:(1)∠BAE=∠CEF;(2)AE=EF.
如圖,四邊形ABCD為菱形,∠C=120°,點(diǎn)E是BC上一點(diǎn).∠AEF=60°,EF交CD于F,求證:(1)∠BAE=∠CEF;(2)AE=EF.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com