
分析 設abc=k再設ab+a+1=u,bc+b+1=v,ac+c+1=w根據(jù)已知條件,$\frac{a}{u}$+$\frac{b}{v}$+$\frac{c}{w}$=1,通過化簡即可得到結果.
解答 解:設abc=k
再設ab+a+1=u,bc+b+1=v,ac+c+1=w
以上三式兩邊分別乘以c,a,b可得:
abc+ca+c=cu,代入abc=k并根據(jù)ac+c+1=w得到:k-1+w=cu①,
abc+ab+a=av,代入abc=k并根據(jù)ab+a+1=u得到:k-1+u=av②,
abc+bc+b=bw,代入abc=k并根據(jù)bc+b+1=v得到:k-1+v=bw③,
根據(jù)已知條件,$\frac{a}{u}$+$\frac{b}{v}$+$\frac{c}{w}$=1,
兩邊同乘以uvw,得到avw+buw+cuv=uvw,
下面把①式兩邊乘以v,②式兩邊乘以w,③式兩邊乘以u,三式相加得到
(k-1)(u+v+w)+uv+vw+uw=avw+buw+cuv=uvw④
①②③三式相乘,可得:(k-1+u)(k-1+v)(k-1+w)=abcuvw=kuvw,
等號左邊把(k-1)看作一項展開,把右邊的kuvw移到左邊,就有:
(k-1)3+(u+v+w)(k-1)2+(uv+vw+uw)(k-1)-uvw(k-1)=0
(k-1)[(k-1)2+(u+v+w)(k-1)+(uv+vw+uw)-uvw]=0⑤,
把④代入⑤化簡為:(k-1)3=0,
所以k=1,
即abc=1.
故答案為:1.
點評 本題考查了分式的加減法,正確的化簡是解題的關鍵.


科目:初中數(shù)學 來源: 題型:解答題
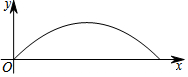 某校足球隊在一次訓練中,一球員從高2.4米的球門正前方m米處將球射向球門,球射向球門的路線呈拋物線,當球飛行的水平距離為6米時,球達到最高點,此時球離地面3米,建立如圖所示的平面直角坐標系
某校足球隊在一次訓練中,一球員從高2.4米的球門正前方m米處將球射向球門,球射向球門的路線呈拋物線,當球飛行的水平距離為6米時,球達到最高點,此時球離地面3米,建立如圖所示的平面直角坐標系查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
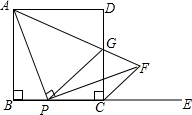 如圖,在正方形ABCD中,AB=a,P為邊BC上一動點(不與B、C重合),E是邊BC延長線上一點,連結AP,過點P作PF⊥AP交∠DCE的平分線于點F,連結AF與邊CD交于點G,連結PG.
如圖,在正方形ABCD中,AB=a,P為邊BC上一動點(不與B、C重合),E是邊BC延長線上一點,連結AP,過點P作PF⊥AP交∠DCE的平分線于點F,連結AF與邊CD交于點G,連結PG.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 正多邊形的外接圓的圓心,就是它的中心 | |
| B. | 正多邊形的外接圓的半徑,就是它的半徑 | |
| C. | 正多邊形的內切圓的半徑,就是它的邊心距 | |
| D. | 正多邊形的外接圓的圓心角,就是它的中心角 |
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com