
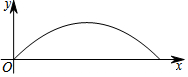
 某校足球隊在一次訓練中,一球員從高2.4米的球門正前方m米處將球射向球門,球射向球門的路線呈拋物線,當球飛行的水平距離為6米時,球達到最高點,此時球離地面3米,建立如圖所示的平面直角坐標系
某校足球隊在一次訓練中,一球員從高2.4米的球門正前方m米處將球射向球門,球射向球門的路線呈拋物線,當球飛行的水平距離為6米時,球達到最高點,此時球離地面3米,建立如圖所示的平面直角坐標系分析 (1)設拋物線的解析式為y=a(x-6)2+3,將(0,0)代入可得;
(2)求出x=10時y的值,判斷即可;
(3)分別求出y=0和y=12時x的值即可知其范圍.
解答 解:(1)設拋物線的解析式為y=a(x-6)2+3,
將點(0,0)代入,得:36a+3=0,
解得:a=-$\frac{1}{12}$,
∴拋物線解析式為y=-$\frac{1}{12}$(x-6)2+3;
(2)當m=10即x=10時,y=-$\frac{1}{12}$(10-6)2+3=$\frac{5}{3}$,
∵0<$\frac{5}{3}$<2.4,
∴足球能射入球門;
(3)當y=0時,-$\frac{1}{12}$(x-6)2+3=0,
解得:x=0或x=12;
當y=2.4時,-$\frac{1}{12}$(x-6)2+3=2.4,
解得:x=6+$\frac{6\sqrt{5}}{5}$或x=6-$\frac{6\sqrt{5}}{5}$,
∴6+$\frac{6\sqrt{5}}{5}$≤x≤12,
即t1的最小值為6+$\frac{6\sqrt{5}}{5}$,t2的最大值為12.
點評 本題主要考查二次函數的應用,根據題意弄清球不過球門時對應的函數值的狀態是關鍵.


科目:初中數學 來源: 題型:解答題
 如圖,一塊矩形綠地ABCD由籬笆圍著,并且由一條與AB邊平行的籬笆EF分開,已知AB=xm,籬笆的總長為600m.
如圖,一塊矩形綠地ABCD由籬笆圍著,并且由一條與AB邊平行的籬笆EF分開,已知AB=xm,籬笆的總長為600m.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| 信件質量x(克) | 0<x≤20 | 20<x≤40 | 40<x≤60 |
| 郵資y/(元/封) | 1.20 | 2.40 | 3.60 |
| A. |  | B. | 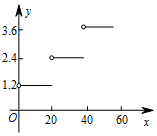 | ||
| C. | 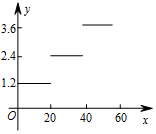 | D. |  |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 點C在⊙A內 | B. | 點C不一定在⊙A外 | C. | 點C在⊙A上 | D. | 點C在⊙A外 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖AB∥CD,AC平分∠BAD,BD平分∠ADC,AC和BD交于點E,F為AD的中點,連結EF.
如圖AB∥CD,AC平分∠BAD,BD平分∠ADC,AC和BD交于點E,F為AD的中點,連結EF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
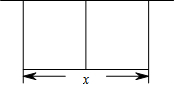 某農場擬建兩間矩形種牛飼養室,飼養室的一面靠現有墻(墻長>50m),中間用一道墻隔開(如圖),己知計劃中的建筑材料可建圍墻的總長為50m,設兩飼養室合計長x(m),總占地面積為y(m2)
某農場擬建兩間矩形種牛飼養室,飼養室的一面靠現有墻(墻長>50m),中間用一道墻隔開(如圖),己知計劃中的建筑材料可建圍墻的總長為50m,設兩飼養室合計長x(m),總占地面積為y(m2)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y隨x的增大而增大 | B. | 圖象經過點(3,-1) | ||
| C. | 圖象不經過第二象限 | D. | 圖象與函數y=-x圖象有一個交點 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com