
 如圖AB∥CD,AC平分∠BAD,BD平分∠ADC,AC和BD交于點E,F為AD的中點,連結EF.
如圖AB∥CD,AC平分∠BAD,BD平分∠ADC,AC和BD交于點E,F為AD的中點,連結EF.分析 (1)圖中△ADC,△AFE,△DFE都,△ADB是等腰三角形.根據等腰三角形的判定方法一一證明即可.
(2)求出AB的長,再根據三角形的中位線定理即可解決問題.
解答 解:(1)圖中△ADC,△AFE,△DFE都,△ADB是等腰三角形.
理由:∵CD∥AB,
∴∠C=∠BAC,
∵∠DAC=∠CAB,
∴∠C=∠DAC,
∴△DAC是等腰三角形,
∵DB平分∠ADC,
∴DB⊥AC,
∴∠AED=90°,
∵AF=FD,
∴EF=AF=FD,
∴△AEF,△DFE都是等腰三角形.
∵∠AED=∠AEB=90°,
∴∠DAE+∠ADE=90°,∠EAB+∠B=90°,
∵∠DAE=∠EAB,
∴∠ADE=∠B,
∴△ADB是等腰三角形.
(2)∵AD=AB,AE⊥BD,
∴DE=EB=6,
在Rt△AEB中,AB=$\sqrt{A{E}^{2}+E{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵DF=FA,DE=EB,
∴EF=$\frac{1}{2}$AB=5.
點評 本題考查等腰三角形的判定和性質、三角形的中位線定理,勾股定理等知識,解題的關鍵是靈活運用所學知識解決問題,需要用轉化的思想思考問題,屬于中考常考題型.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 該事件是必然事件 | B. | 該事件是不可能事件 | ||
| C. | 該事件是不確定事件 | D. | 該事件發生的可能性很大 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
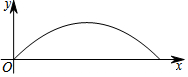 某校足球隊在一次訓練中,一球員從高2.4米的球門正前方m米處將球射向球門,球射向球門的路線呈拋物線,當球飛行的水平距離為6米時,球達到最高點,此時球離地面3米,建立如圖所示的平面直角坐標系
某校足球隊在一次訓練中,一球員從高2.4米的球門正前方m米處將球射向球門,球射向球門的路線呈拋物線,當球飛行的水平距離為6米時,球達到最高點,此時球離地面3米,建立如圖所示的平面直角坐標系查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $2\sqrt{10}$ | B. | 12 | C. | 2$\sqrt{10}$+10 | D. | 12或2$\sqrt{10}$+10 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com