
 已知,如圖,在Rt△ABC中,AC=6,BC=8,D邊AB上一點,連接CD,過點D作DE⊥DC交BC于E,把△BDE沿DE翻折得△DEB1,連接B1C.
已知,如圖,在Rt△ABC中,AC=6,BC=8,D邊AB上一點,連接CD,過點D作DE⊥DC交BC于E,把△BDE沿DE翻折得△DEB1,連接B1C.分析 (1)由折疊的性質得∠BDE=∠B1DE,由垂直的定義得到DE⊥DC,根據余角的性質即可得到∠ADC=∠B1DC;
(2)延長B1E交AB于F,根據全等三角形的判定定理得到△BDG≌△B1FD,由全等三角形的性質得到DF=DG,
推出△ADC≌△GDC,根據全等三角形的性質得到DG=AD,等量代換得到DF=AD=DG,設DF=AD=DG=x,求得BF=8-2x,根據相似三角形的性質得到EF=$\frac{12-3x}{2}$,
由于△EFD∽△ACD,得到$\frac{DF}{AC}$=$\frac{EF}{AD}$,求得BF=3,EF=$\frac{3}{2}$,于是得到結論;
(3)設AD=x,則CD=$\sqrt{{x}^{2}+36}$,BD=8-x,①當B1D=B1C時,則∠B1DC=∠B1CD,根據折疊的性質得到DB1=BD=8-x,過B1作B1F⊥CD,求得DF=CF=$\frac{1}{2}$CD=$\frac{\sqrt{{x}^{2}+36}}{2}$,根據相似三角形的性質得到$\frac{{B}_{1}D}{CD}$=$\frac{DF}{AD}$,即$\frac{8-x}{\sqrt{{x}^{2}+36}}$=$\frac{\frac{\sqrt{{x}^{2}+36}}{2}}{x}$,由此方程無實數根,得到B1D≠B1C,②B1D=CD時,得到B1D=CD=BD=8-x,根據勾股定理列方程得到結論;③當CD=B1C時,過C作CH⊥DB1,根據全等三角形的性質得到AD=DH=x,于是得到結論.
解答 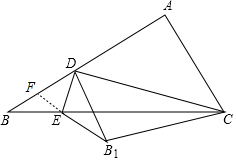 (1)證明:由折疊的性質得:∠BDE=∠B1DE,
(1)證明:由折疊的性質得:∠BDE=∠B1DE,
∵DE⊥DC,
∴∠ADC=180°-90°-∠BDE=90°-∠BDE,∠B1DC=90-∠B1DE,
∴∠ADC=∠B1DC;
(2)解:延長B1E交AB于F,
∵B1E∥AC,∠A=90°,
∴B1F⊥AB,
∴∠EB1D+∠BDB1=90°,
∵∠B=∠EB1D,
∴∠B+BDB1=90°,
∴∠BGD=90°,
在△BDG和△B1FD中,$\left\{\begin{array}{l}{∠B=∠E{B}_{1}D}\\{∠BGD=∠{B}_{1}FD}\\{BD=D{B}_{1}}\end{array}\right.$,
∴△BDG≌△B1FD,
∴DF=DG,
在△ADC和△GDC中,$\left\{\begin{array}{l}{∠ADC=∠CDG}\\{∠A=∠DGC=90°}\\{DC=DC}\end{array}\right.$,
∴△ADC≌△GDC,
∴DG=AD,
∴DF=AD=DG,
設DF=AD=DG=x,
∴BF=8-2x,
∵EF∥AC,
∴△BFE∽△BAC,
∴$\frac{EF}{AC}$=$\frac{BF}{AB}$,
∴EF=$\frac{12-3x}{2}$,
∵△EFD∽△ACD,
∴$\frac{DF}{AC}$=$\frac{EF}{AD}$,
∴$\frac{x}{6}$=$\frac{\frac{12-3x}{2}}{x}$,
解得:x=3,
∴BF=3,EF=$\frac{3}{2}$,
∴DE=$\frac{3\sqrt{5}}{2}$;
(3)解:設AD=x,
則CD=$\sqrt{{x}^{2}+36}$,BD=8-x,
∵△B1CD是等腰三角形,
①當B1D=B1C時,則∠B1DC=∠B1CD,
∴DB1=BD=8-x,
如圖2,過B1作B1F⊥CD,
則DF=CF=$\frac{1}{2}$CD=$\frac{\sqrt{{x}^{2}+36}}{2}$,
∵∠ADC=∠B1DC,∠B1FD=∠A=90°,
∴△CDA∽△B1DC,
∴$\frac{{B}_{1}D}{CD}$=$\frac{DF}{AD}$,即$\frac{8-x}{\sqrt{{x}^{2}+36}}$=$\frac{\frac{\sqrt{{x}^{2}+36}}{2}}{x}$,
∴3x2-16x+36=0,
∵此方程無實數根,
∴B1D≠B1C,
②B1D=CD時,
∴B1D=CD=BD=8-x,
∴(8-x)2=x2+62,
∴x=$\frac{7}{4}$,
∴AD=$\frac{7}{4}$,
③當CD=B1C時,如圖2,過C作CH⊥DB1,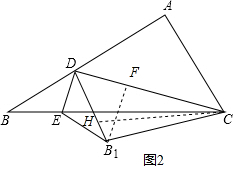
則DH=B1H=$\frac{1}{2}$DB1=$\frac{1}{2}$BD=$\frac{1}{2}$(8-x),
在△ACD和△CHD中$\left\{\begin{array}{l}{∠ADC=∠CDH}\\{∠A=∠CHD=90°}\\{CD=CD}\end{array}\right.$,
∴△ACD≌△CHD,
∴AD=DH=x,
∴x=$\frac{1}{2}$(8-x),
∴x=$\frac{8}{3}$,
∴AD=$\frac{8}{3}$,
綜上所述:當△B1CD是等腰三角形時,AD的長為$\frac{7}{4}$或$\frac{8}{3}$.
點評 本題考查了全等三角形的判斷和性質,相似三角形的判定和性質,勾股定理等腰三角形的性質,正確的理解題意是解題的關鍵.


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:初中數學 來源: 題型:解答題
 已知直線y=-2x+4與x軸、y軸分別交于A、D兩點,拋物線y=ax2-x+c經過點A、D,點B是拋物線與x軸的另一個交點.
已知直線y=-2x+4與x軸、y軸分別交于A、D兩點,拋物線y=ax2-x+c經過點A、D,點B是拋物線與x軸的另一個交點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 底邊對應相等的兩個等腰三角形全等 | |
| B. | 腰對應相等的兩個等腰三角形全等 | |
| C. | 斜邊對應相等的兩個直角三角形全等 | |
| D. | 面積相等的兩個等邊三角形全等 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 80-x=30%×(180+x) | B. | 80-x=30%×180 | C. | 180+x=30%×(80-x) | D. | 80-x=30%×260 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com