
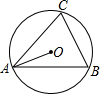
 如圖,△ABC內(nèi)接于⊙O,若∠OAB=20°,則∠C的大小為70度.
如圖,△ABC內(nèi)接于⊙O,若∠OAB=20°,則∠C的大小為70度. 分析 連接OB.根據(jù)等腰△OAB的兩個(gè)底角∠OAB=∠OBA、三角形的內(nèi)角和定理求得∠AOB的度數(shù),然后由圓周角定理求即可得∠C的度數(shù).
解答 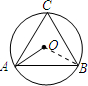 解:連接OB.
解:連接OB.
在△OAB中,OA=OB(⊙O的半徑),
∴∠OAB=∠OBA(等邊對等角);
又∵∠OAB=20°,
∴∠OBA=20°;
∴∠AOB=180°-2×20°=140°;
而∠C=$\frac{1}{2}$∠AOB(同弧所對的圓周角是所對的圓心角的一半),
∴∠C=70°,
故答案是:70.
點(diǎn)評 本題主要考查了三角形的內(nèi)角和定理、圓周角定理.解答此類題目時(shí),經(jīng)常利用圓的半徑都相等的性質(zhì),將圓心角置于等腰三角形中解答.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 已知,如圖,在Rt△ABC中,AC=6,BC=8,D邊AB上一點(diǎn),連接CD,過點(diǎn)D作DE⊥DC交BC于E,把△BDE沿DE翻折得△DEB1,連接B1C.
已知,如圖,在Rt△ABC中,AC=6,BC=8,D邊AB上一點(diǎn),連接CD,過點(diǎn)D作DE⊥DC交BC于E,把△BDE沿DE翻折得△DEB1,連接B1C.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
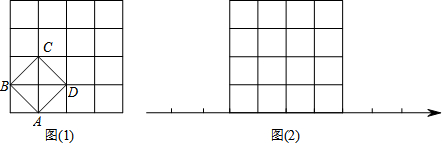
 如圖,在△ABC中,DE∥BC,分別交AB、AC于點(diǎn)D,E.若DE=4,$\frac{AD}{DB}$=$\frac{2}{3}$,則下列選項(xiàng)中錯(cuò)誤的是( )
如圖,在△ABC中,DE∥BC,分別交AB、AC于點(diǎn)D,E.若DE=4,$\frac{AD}{DB}$=$\frac{2}{3}$,則下列選項(xiàng)中錯(cuò)誤的是( )| A. | △ADE∽△ABC | B. | BC=10 | ||
| C. | $\frac{△ADE的周長}{△ABC的周長}$=$\frac{2}{3}$ | D. | $\frac{△ADE的面積}{四邊形DBCE的面積}$=$\frac{4}{21}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
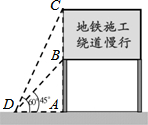 某市備受關(guān)注的地鐵六號線正緊張施工,為了緩解一些施工路段交通擁擠的現(xiàn)狀,交警隊(duì)設(shè)立了如圖所示的交通略況顯示牌,已知立桿AB的高度是3m,從側(cè)面D點(diǎn)測得顯示牌頂端C點(diǎn)和底端B點(diǎn)的仰角分別是60°和45°,求路況顯示牌BC的高度.
某市備受關(guān)注的地鐵六號線正緊張施工,為了緩解一些施工路段交通擁擠的現(xiàn)狀,交警隊(duì)設(shè)立了如圖所示的交通略況顯示牌,已知立桿AB的高度是3m,從側(cè)面D點(diǎn)測得顯示牌頂端C點(diǎn)和底端B點(diǎn)的仰角分別是60°和45°,求路況顯示牌BC的高度.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | p=3,q=1 | B. | p=-3,q=-9 | C. | p=0,q=0 | D. | p=-3,q=1 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com