
 如圖,在△ABC中,DE∥BC,分別交AB、AC于點D,E.若DE=4,$\frac{AD}{DB}$=$\frac{2}{3}$,則下列選項中錯誤的是( )
如圖,在△ABC中,DE∥BC,分別交AB、AC于點D,E.若DE=4,$\frac{AD}{DB}$=$\frac{2}{3}$,則下列選項中錯誤的是( )| A. | △ADE∽△ABC | B. | BC=10 | ||
| C. | $\frac{△ADE的周長}{△ABC的周長}$=$\frac{2}{3}$ | D. | $\frac{△ADE的面積}{四邊形DBCE的面積}$=$\frac{4}{21}$ |
分析 根據題意可以得到△ADE∽△ABC,然后根據題目中的條件即可推出選項中的說法是否正確,從而可以解答本題.
解答 解:∵在△ABC中,DE∥BC,
∴△ADE∽△ABC,故選項A正確,
∴$\frac{AD}{AB}=\frac{DE}{BC}$=$\frac{△ADE的周長}{△ABC的周長}$,$\frac{△ADE的面積}{△ABC的面積}=(\frac{AD}{AB})^{2}$,
∵DE=4,$\frac{AD}{DB}$=$\frac{2}{3}$,
∴$\frac{AD}{AB}=\frac{2}{5}$,
∴AB=10,$\frac{△ADE的周長}{△ABC的周長}$=$\frac{2}{5}$,$\frac{△ADE的面積}{△ABC的面積}=(\frac{AD}{AB})^{2}$=$\frac{4}{25}$,故選項B正確,選項C錯誤,
∴$\frac{△ADE的面積}{四邊形DBCE的面積}=\frac{4}{21}$,故選項D正確,
故選C.
點評 本題考查相似三角形的判定與性質,解答本題的關鍵是明確題意,找出所求問題需要的條件,利用相似三角形的性質解答問題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:選擇題
| A. | 5cm | B. | $\frac{25}{π}$cm | C. | 10cm | D. | 25cm |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y3>y2>y1 | B. | y1>y2>y3 | C. | y1>y3>y2 | D. | y3>y1>y2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
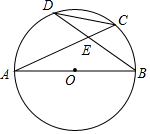 如圖所示,AB是⊙O的直徑,弦AC、BD相交于點E,且C為弧BD的中點.若EC=2,tan∠CEB=2.
如圖所示,AB是⊙O的直徑,弦AC、BD相交于點E,且C為弧BD的中點.若EC=2,tan∠CEB=2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 (1)①計算125°24′-60°36′(結果用度表示);
(1)①計算125°24′-60°36′(結果用度表示);查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com