
分析 (1)先變號,再進行分式的加減即可;
(2)先通分,再進行分式的加減即可;
(3)先把分子分母因式分解再約分即可;
(4)先通分,再進行分式的加減即可.
解答 解:(1)原式=$\frac{x+2y}{{x}^{2}-{y}^{2}}$-$\frac{y}{{x}^{2}-{y}^{2}}$-$\frac{2x}{{x}^{2}-{y}^{2}}$
=$\frac{x+2y-y-2x}{{x}^{2}-{y}^{2}}$
=$\frac{y-x}{(x+y)(x-y)}$
=-$\frac{1}{x+y}$;
(2)原式=$\frac{{a}^{2}-{b}^{2}}{a+b}$+$\frac{2{b}^{2}}{a+b}$
=$\frac{{a}^{2}+{b}^{2}}{a+b}$;
(3)原式=$\frac{(a+1)(a-1)}{(a+3)^{2}}$•$\frac{1}{a+1}$•$\frac{(a+3)(a-3)}{a-1}$
=$\frac{a-3}{a+3}$;
(4)原式=$\frac{x(x+2)-x(x-2)}{(x+2)(x-2)}$•$\frac{x-2}{4x}$
=$\frac{1}{x+2}$.
點評 本題考查了分式的混合運算,掌握分式的通分、約分是解題的關鍵.


科目:初中數學 來源: 題型:解答題
| 購物金額(原價) | 優惠率 |
| 不超過3000元的部分 | 無優惠 |
| 超過3000元但不超過10000元部分 | 5% |
| 超過10000元的部分 | 10% |
| 付款時,還可以享受單筆消費滿2000元立減160元優惠 | |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
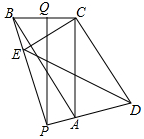 如圖,在△ABC中,∠ACB=90°,BC=6,AC=8,將△ABC繞C點旋轉一個角度到△DEC,直線AD,EB交于P點,Q是BC的中點,連PQ,在旋轉過程中,求:
如圖,在△ABC中,∠ACB=90°,BC=6,AC=8,將△ABC繞C點旋轉一個角度到△DEC,直線AD,EB交于P點,Q是BC的中點,連PQ,在旋轉過程中,求:查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com