
 如圖,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB邊上一動點,PD⊥AC于點D,點E在P的右側,且PE=1,連結CE.P從點A出發,沿AB方向運動,當E到達點B時,P停止運動.在整個運動過程中,陰影部分面積S1+S2的大小變化情況是( )
如圖,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB邊上一動點,PD⊥AC于點D,點E在P的右側,且PE=1,連結CE.P從點A出發,沿AB方向運動,當E到達點B時,P停止運動.在整個運動過程中,陰影部分面積S1+S2的大小變化情況是( )| A. | 一直不變 | B. | 一直減小 | C. | 一直增大 | D. | 先減小后增大 |
分析 設AP=x,則DP=$\frac{1}{2}$x,則BE=1-x,然后再求得點C到AB的距離,從而可可得到S1+S2與x的函數關系,然后依據二次函數的性質求解即可.
解答 解:∵∠ACB=90°,∠A=30°,BC=1,
∴AB=2.
依據勾股定理可知:AC=$\sqrt{3}$.
設點C到AB的距離為h,則2h=1×$\sqrt{3}$,解得:h=$\frac{\sqrt{3}}{2}$.
所以S1+S2=$\frac{1}{2}$DP•AD+$\frac{1}{2}$BE•h=$\frac{1}{2}$×$\frac{1}{2}$x×$\frac{\sqrt{3}}{2}$x+$\frac{1}{2}$(1-x)×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{8}$x2-$\frac{1}{2}$x+$\frac{1}{2}$.
對稱軸為x=$\frac{2\sqrt{3}}{3}$>1.
∵AB=2,PE=1,
∴0<x<0,
所以S1+S2的值一直減小.
故選:B.
點評 本題主要考查的是含30°直角三角形的性質,三角形的面積,二次函數的最值,根據題意列出S1+S2與x的函數關系是解題的關鍵.


科目:初中數學 來源: 題型:填空題
 如圖,已知∠MON=80°,OE平分∠MON,點A、B、C分別是射線OM、OE、ON上的動點(A、B、C不與點O重合),連接AC交射線OE于點D.當AB⊥OM,且△ADB有兩個相等的角時,∠OAC的度數為10°、25°、40°.
如圖,已知∠MON=80°,OE平分∠MON,點A、B、C分別是射線OM、OE、ON上的動點(A、B、C不與點O重合),連接AC交射線OE于點D.當AB⊥OM,且△ADB有兩個相等的角時,∠OAC的度數為10°、25°、40°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,⊙O是四邊形ABCD的內切圓,切點為E,F,G,H,已知AD∥BC,AB=CD,DO=6cm,CO=8cm,求四邊形ABCD的周長.
如圖,⊙O是四邊形ABCD的內切圓,切點為E,F,G,H,已知AD∥BC,AB=CD,DO=6cm,CO=8cm,求四邊形ABCD的周長.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,四邊形ABCD的邊AB、BC、CD、DA和⊙O分別切于L、M、N、P,且AB=10cm,CD=5cm,則四邊形ABCD周長為30cm.
如圖,四邊形ABCD的邊AB、BC、CD、DA和⊙O分別切于L、M、N、P,且AB=10cm,CD=5cm,則四邊形ABCD周長為30cm.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
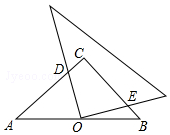 如圖,在等腰直角△ABC中,∠C=90°,點O是AB的中點,且AC=1,將一塊直角三角板的直角頂點放在點O處,始終保持該直角三角板的兩直角邊分別與AC、BC相交,交點分別為D、E,則CD+CE=1.
如圖,在等腰直角△ABC中,∠C=90°,點O是AB的中點,且AC=1,將一塊直角三角板的直角頂點放在點O處,始終保持該直角三角板的兩直角邊分別與AC、BC相交,交點分別為D、E,則CD+CE=1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
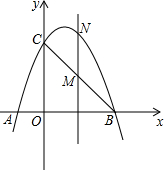 如圖,已知拋物線經過點A(-1,0),B(3,0),C(0,3)三點.
如圖,已知拋物線經過點A(-1,0),B(3,0),C(0,3)三點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com