
 如圖,⊙O是四邊形ABCD的內切圓,切點為E,F,G,H,已知AD∥BC,AB=CD,DO=6cm,CO=8cm,求四邊形ABCD的周長.
如圖,⊙O是四邊形ABCD的內切圓,切點為E,F,G,H,已知AD∥BC,AB=CD,DO=6cm,CO=8cm,求四邊形ABCD的周長. 分析 首先證明AB+CD=BC+AD,再證明∠DOC=90°,理由勾股定理求出CD,即可解決問題.
解答 解:如圖,
∵⊙O是四邊形ABCD的內切圓,切點為E,F,G,H,
∴AF=AG,BH=BG,CH=CE,DE=DF,
∴BH+CH+AF+DF=BG+CE+AG+DE,
即BC+AD=AB+CD,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵∠ODE=$\frac{1}{2}$∠ADC,∠OCD=$\frac{1}{2}$∠DCB,
∴∠ODC+∠OCD=90°,
∴∠DOC=90°,
在Rt△DOC中,CD=$\sqrt{O{D}^{2}+O{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵AB=CD=10,
∴AB+CD=BC+AD=20,
∴四邊形ABCD的周長為20.
點評 此題主要考查了切線長定理、平行線的性質、直角三角形的判定、勾股定理等知識,正確利用切線長定理得出相等的線段是解題關鍵,記住本題的結論:圓的外切四邊形對邊和相等.


科目:初中數學 來源: 題型:填空題
 將1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如圖方式排列,若規定(m,n)表示第m排的第n個數,如(4,2)表示的數是 $\sqrt{6}$,則(5,4)與(18,15)表示的兩數之積是2$\sqrt{3}$.
將1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如圖方式排列,若規定(m,n)表示第m排的第n個數,如(4,2)表示的數是 $\sqrt{6}$,則(5,4)與(18,15)表示的兩數之積是2$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
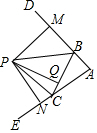 如圖,∠DBC和∠ECB是△ABC的兩個外角,點P是∠DBC、∠ECB兩角的平分線的交點,PM、PN、PQ分別是P點到AB、AC、BC三邊的垂線段,PM、PN、PQ的數量關系為( )
如圖,∠DBC和∠ECB是△ABC的兩個外角,點P是∠DBC、∠ECB兩角的平分線的交點,PM、PN、PQ分別是P點到AB、AC、BC三邊的垂線段,PM、PN、PQ的數量關系為( )| A. | PM>PN>PQ | B. | PM<PN<PQ | C. | PM=PN=PQ | D. | PM=PN>PQ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,興修水利開渠,其斷面為等腰梯形,要與水平線的夾角為60°,濕透周長為定制l米(l=AB+BC+CD),問渠深x為$\frac{\sqrt{3}}{4}$l米時,可使水流量最大?
如圖,興修水利開渠,其斷面為等腰梯形,要與水平線的夾角為60°,濕透周長為定制l米(l=AB+BC+CD),問渠深x為$\frac{\sqrt{3}}{4}$l米時,可使水流量最大?查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB邊上一動點,PD⊥AC于點D,點E在P的右側,且PE=1,連結CE.P從點A出發,沿AB方向運動,當E到達點B時,P停止運動.在整個運動過程中,陰影部分面積S1+S2的大小變化情況是( )
如圖,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB邊上一動點,PD⊥AC于點D,點E在P的右側,且PE=1,連結CE.P從點A出發,沿AB方向運動,當E到達點B時,P停止運動.在整個運動過程中,陰影部分面積S1+S2的大小變化情況是( )| A. | 一直不變 | B. | 一直減小 | C. | 一直增大 | D. | 先減小后增大 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{8}$÷$\sqrt{2}$=2 | B. | 5$\sqrt{3}$•5$\sqrt{2}$=5$\sqrt{6}$ | C. | 2$\sqrt{3}$+3$\sqrt{2}$=5$\sqrt{6}$ | D. | $\sqrt{(-6)^{2}}$=-6 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com