
 如圖,興修水利開渠,其斷面為等腰梯形,要與水平線的夾角為60°,濕透周長為定制l米(l=AB+BC+CD),問渠深x為$\frac{\sqrt{3}}{4}$l米時,可使水流量最大?
如圖,興修水利開渠,其斷面為等腰梯形,要與水平線的夾角為60°,濕透周長為定制l米(l=AB+BC+CD),問渠深x為$\frac{\sqrt{3}}{4}$l米時,可使水流量最大? 分析 設橫截面面積為S,由條件知要使流量最大,只要求橫截面積最大即可,作AE⊥BC,則AE=DF=x,利用三角函數求得AB=CD=$\frac{AE}{sin60°}$=$\frac{2\sqrt{3}}{3}$x、BE=$\frac{AE}{tan60°}$=$\frac{\sqrt{3}}{3}$x,根據l=AB+BC+CD得BC=l-(AB+CD)=l-$\frac{4\sqrt{3}}{3}$x,AD=BC+2BE=l-$\frac{4\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$x=1-$\frac{2\sqrt{3}}{3}$x,根據梯形面積公式求得S=$\frac{1}{2}$(1-$\frac{2\sqrt{3}}{3}$x+l-$\frac{4\sqrt{3}}{3}$x)•x=-$\frac{2\sqrt{3}}{3}$x2+lx,由二次函數的性質得出其最值情況可得答案.
解答 解:設橫截面面積為S,由條件知要使流量最大,只要求橫截面積最大即可.
過點A作AE⊥BC于點E,作DF⊥BC于點F,
則AE=DF=x,
則AB=CD=$\frac{AE}{sin60°}$=$\frac{2\sqrt{3}}{3}$x,BE=$\frac{AE}{tan60°}$=$\frac{\sqrt{3}}{3}$x,
∵濕透周長為定制l米(l=AB+BC+CD),
∴BC=l-(AB+CD)=l-$\frac{4\sqrt{3}}{3}$x,AD=BC+2BE=l-$\frac{4\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$x=1-$\frac{2\sqrt{3}}{3}$x,
∴S=$\frac{1}{2}$(1-$\frac{2\sqrt{3}}{3}$x+l-$\frac{4\sqrt{3}}{3}$x)•x=-$\frac{2\sqrt{3}}{3}$x2+lx,
則當x=-$\frac{l}{2×(-\frac{2\sqrt{3}}{3})}$=$\frac{\sqrt{3}}{4}$l時,S取得最大值,
故答案為:$\frac{\sqrt{3}}{4}$l.
點評 本題主要考查二次函數的應用,根據題意明確要使流量最大,只要求橫截面積最大是解題的根本,由題中數據表示出梯形的上下底的長是解題的關鍵.


科目:初中數學 來源:2016-2017學年北京市西城區七年級上學期期末考試數學試卷(解析版) 題型:解答題
自2014年12月28日北京公交地鐵調價以來,人們的出行成本發生了較大的變化. 小林根據新聞,將地鐵和公交車的票價繪制成了如下兩個表格。(說明:表格中“6~12公里”指的是大于6公里,小于等于12公里,其他類似)
|
|
根據以上信息回答下列問題:
小林辦了一張市政交通一卡通學生卡,目前乘坐地鐵沒有折扣。
(1)如果小林全程乘坐地鐵的里程為14公里,用他的學生卡需要刷卡交費________元;
(2)如果小林全程乘坐公交車的里程為16公里,用他的學生卡需要刷卡交________元;
(3)小林用他的學生卡乘坐一段地鐵后換乘公交車,兩者累計里程為12公里。已知他乘坐地鐵平均每公里花費0.4元,乘坐公交車平均每公里花費0.25元,此次行程共花費4.5元。請問小林乘坐地鐵和公交車的里程分別是多少公里?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
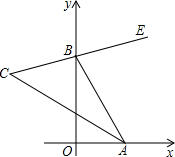 如圖,在平面直角坐標系中,點A與點B分別在x軸與y軸的正半軸上移動,BE是∠ABy的平分線,BE的反向延長線與∠OAB的平分線相交于點C,試問∠C的大小是否隨點A、B的移動而發生變化?如果保持不變,求出∠C的大小;如果隨點A、B的移動而發生變化,請求出變化范圍.
如圖,在平面直角坐標系中,點A與點B分別在x軸與y軸的正半軸上移動,BE是∠ABy的平分線,BE的反向延長線與∠OAB的平分線相交于點C,試問∠C的大小是否隨點A、B的移動而發生變化?如果保持不變,求出∠C的大小;如果隨點A、B的移動而發生變化,請求出變化范圍.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,⊙O是四邊形ABCD的內切圓,切點為E,F,G,H,已知AD∥BC,AB=CD,DO=6cm,CO=8cm,求四邊形ABCD的周長.
如圖,⊙O是四邊形ABCD的內切圓,切點為E,F,G,H,已知AD∥BC,AB=CD,DO=6cm,CO=8cm,求四邊形ABCD的周長.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,四邊形ABCD的邊AB、BC、CD、DA和⊙O分別切于L、M、N、P,且AB=10cm,CD=5cm,則四邊形ABCD周長為30cm.
如圖,四邊形ABCD的邊AB、BC、CD、DA和⊙O分別切于L、M、N、P,且AB=10cm,CD=5cm,則四邊形ABCD周長為30cm.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (x+2y)(x-2y)=x2-4y2 | B. | x2y-xy2-1=xy(x-y)-1 | ||
| C. | a2-4ab+4b2=(a-2b)2 | D. | 2a2-2a=2a2(1-$\frac{1}{a}$) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com