
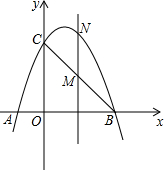 如圖,已知拋物線經過點A(-1,0),B(3,0),C(0,3)三點.
如圖,已知拋物線經過點A(-1,0),B(3,0),C(0,3)三點.分析 (1)利用待定系數法求二次函數的解析式;
(2)先求直線BC的解析式,表示出M、N兩點的坐標,利用縱坐標的差計算MN的長即可;
(3)根據面積公式得:S△BNC=S△CMN+S△MNB=$\frac{1}{2}$|MN|•|OB|,OB的長是定值為3,所以MN的最大值即為面積的最大值,求MN所表示的二次函數的最值即可.
解答 解:(1)∵拋物線經過點A(-1,0),B(3,0),C(0,3)三點,
∴設拋物線的解析式為:y=a(x+1)(x-3),
把C(0,3)代入得:3=a(0+1)(0-3),
a=-1,
∴y拋物線的解析式:y=-x2+2x+3;
(2)設直線BC的解析式為:y=kx+b,
把B(3,0),C(0,3)代入得:$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直線BC的解析式為y=-x+3,
∴M(m,-m+3),
又∵MN⊥x軸,
∴N(m,-m2+2m+3),
∴MN=(-m2+2m+3)-(-m+3)=-m2+3m(0<m<3);
(3)存在,
S△BNC=S△CMN+S△MNB=$\frac{1}{2}$|MN|•|OB|,
∴當|MN|最大時,△BNC的面積最大,
MN=-m2+3m=-(m-$\frac{3}{2}$)2+$\frac{9}{4}$,
當m=$\frac{3}{2}$時,MN的有最大值為$\frac{9}{4}$,
所以當m=$\frac{3}{2}$時,△BNC的面積最大為$\frac{1}{2}$×$\frac{9}{4}$×3=$\frac{27}{8}$.
點評 本題是二次函數的綜合題,難度適中,考查了利用待定系數法求二次函數和一次函數的解析式,并利用鉛直高度與水平寬度的積求三角形的面積,同時要熟練掌握二次函數的最值的求法.


 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:選擇題
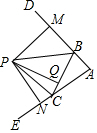 如圖,∠DBC和∠ECB是△ABC的兩個外角,點P是∠DBC、∠ECB兩角的平分線的交點,PM、PN、PQ分別是P點到AB、AC、BC三邊的垂線段,PM、PN、PQ的數量關系為( )
如圖,∠DBC和∠ECB是△ABC的兩個外角,點P是∠DBC、∠ECB兩角的平分線的交點,PM、PN、PQ分別是P點到AB、AC、BC三邊的垂線段,PM、PN、PQ的數量關系為( )| A. | PM>PN>PQ | B. | PM<PN<PQ | C. | PM=PN=PQ | D. | PM=PN>PQ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB邊上一動點,PD⊥AC于點D,點E在P的右側,且PE=1,連結CE.P從點A出發,沿AB方向運動,當E到達點B時,P停止運動.在整個運動過程中,陰影部分面積S1+S2的大小變化情況是( )
如圖,在△ABC中,∠ACB=90°,∠A=30°,BC=1.P是AB邊上一動點,PD⊥AC于點D,點E在P的右側,且PE=1,連結CE.P從點A出發,沿AB方向運動,當E到達點B時,P停止運動.在整個運動過程中,陰影部分面積S1+S2的大小變化情況是( )| A. | 一直不變 | B. | 一直減小 | C. | 一直增大 | D. | 先減小后增大 |
查看答案和解析>>
科目:初中數學 來源:2016-2017學年北京市西城區七年級上學期期末考試數學試卷(解析版) 題型:單選題
下列方程中,解為x=4的方程是( ).
A. x-1=4 B. 4x=1 C. 4x-1=3x+3 D. 2(x-1)=1
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
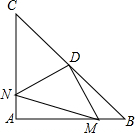 如圖,在Rt△ABC中,AB=AC,∠BAC=90°,D為BC的中點.
如圖,在Rt△ABC中,AB=AC,∠BAC=90°,D為BC的中點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{8}$÷$\sqrt{2}$=2 | B. | 5$\sqrt{3}$•5$\sqrt{2}$=5$\sqrt{6}$ | C. | 2$\sqrt{3}$+3$\sqrt{2}$=5$\sqrt{6}$ | D. | $\sqrt{(-6)^{2}}$=-6 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1207×108元 | B. | 12.07×1010元 | C. | 1.207×108元 | D. | 1.207×1011元 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com