
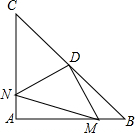
 如圖,在Rt△ABC中,AB=AC,∠BAC=90°,D為BC的中點.
如圖,在Rt△ABC中,AB=AC,∠BAC=90°,D為BC的中點.分析 (1)根據直角三角形的性質可知CD=BD=AD;
(2)連接AD,可證明△ADM≌△CDN,則可證得DM=DN,∠CDN=∠ADM,再利用AD⊥BC,可求得ND⊥MD,可判定△DMN為等腰直角三角形.
解答 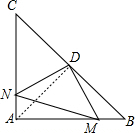 解:
解:
(1)∵在Rt△ABC中,∠BAC=90°,D為BC的中點,
∴CD=BD=AD,
即點D到三個頂點的距離相等;
(2)△DMN為等腰直角三角形,
證明如下:
如圖,連接AD,
由(1)可知CD=AD,
∵AC=AB,
∴AD⊥BC,且∠DAB=∠CAD=45°,
∴∠C=∠DAM,
∵AN=BM,
∴CN=AM,
在△ADM和△CDN中
$\left\{\begin{array}{l}{AD=CD}\\{∠DAM=∠C}\\{AM=CN}\end{array}\right.$
∴△ADM≌△CDN(SAS),
∴DM=DN,且∠ADM=∠CDN,
∴∠ADM+∠ADN=∠ADN+∠NDC=90°,
∴△DMN為等腰直角三角形.
點評 本題主要考查等腰直角三角形、全等三角形的判定和性質,在(1)中掌握直角三角形斜邊上的中線等于斜邊的一半是解題的關鍵,在(2)中證明△ADM≌△CDN是解題的關鍵.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:初中數學 來源: 題型:填空題
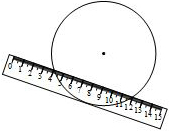 如圖,兩邊平行的刻度尺在圓上移動,當刻度尺的一邊與直徑為10cm的圓相切時,另一邊與圓兩個交點處的讀數恰好為“4”和“12”(單位:cm),則刻度尺的寬為2cm.
如圖,兩邊平行的刻度尺在圓上移動,當刻度尺的一邊與直徑為10cm的圓相切時,另一邊與圓兩個交點處的讀數恰好為“4”和“12”(單位:cm),則刻度尺的寬為2cm.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
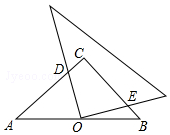 如圖,在等腰直角△ABC中,∠C=90°,點O是AB的中點,且AC=1,將一塊直角三角板的直角頂點放在點O處,始終保持該直角三角板的兩直角邊分別與AC、BC相交,交點分別為D、E,則CD+CE=1.
如圖,在等腰直角△ABC中,∠C=90°,點O是AB的中點,且AC=1,將一塊直角三角板的直角頂點放在點O處,始終保持該直角三角板的兩直角邊分別與AC、BC相交,交點分別為D、E,則CD+CE=1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
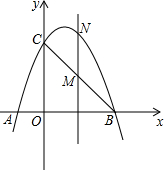 如圖,已知拋物線經過點A(-1,0),B(3,0),C(0,3)三點.
如圖,已知拋物線經過點A(-1,0),B(3,0),C(0,3)三點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 單項式3ab的次數是1 | |
| B. | 單項式$\frac{2ab}{3}$的系數是2 | |
| C. | 3a-2a2b+2ab是三次三項式 | |
| D. | -4a2b,3ab,5是多項式-4a2b+3ab-5的項 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0個 | B. | 1個 | C. | 2個 | D. | 3個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com