
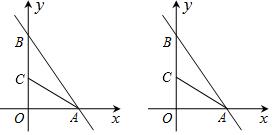
分析 (1)在函數解析式中分別令y=0和x=0,解相應方程,可求得A、B的坐標;
(2)過C作CD⊥AB于點D,由勾股定理可求得AB,由角平分線的性質可得CO=CD,則可用CO表示出△AOB面積,可求得CO,則可求得△ABC的面積;
(3)可設P(x,y),則可分別表示出AP2、BP2,分∠PAB=90°、∠PBA=90°和∠APB=90°三種情況,分別可得到關于x、y的方程組,可求得P點坐標.
解答 解:
(1)在y=-$\frac{4}{3}$x+8中,令y=0可得0=-$\frac{4}{3}$x+8,解得x=6,令x=0,解得y=8,
∴A(6,0),B(0,8);
(2)如圖,過點C作CD⊥AB于點D,
∵AC平分∠OAB,
∴CD=OC,
由(1)可知OA=6,OB=8,
∴AB=10,
∵S△AOB=S△AOC+S△ABC,
∴$\frac{1}{2}$×6×8=$\frac{1}{2}$×6OC+$\frac{1}{2}$×10OC,解得OC=3,
∴S△ABC=$\frac{1}{2}$×10×3=15;
(3)設P(x,y),則AP2=(x-6)2+y2,BP2=x2+(y-8)2,且AB2=100,
∵△PAB為等腰直角三角形,
∴有∠PAB=90°、∠PBA=90°和∠APB=90°三種情況,
①當∠PAB=90°時,則有PA2=AB2且PA2+AB2=BP2,
即$\left\{\begin{array}{l}{(x-6)^{2}+{y}^{2}=100}\\{(x-6)^{2}+{y}^{2}+100={x}^{2}+(y-8)^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=13}\\{y=6}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-6}\end{array}\right.$,
此時P點坐標為(13,6)或(-2,-6);
②∠PBA=90°時,則有PB2=AB2且PB2+AB2=PA2,
即$\left\{\begin{array}{l}{{x}^{2}+(y-8)^{2}=100}\\{{x}^{2}+(y-8)^{2}+100=(x-6)^{2}+{y}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=8}\\{y=14}\end{array}\right.$或$\left\{\begin{array}{l}{x=-8}\\{y=2}\end{array}\right.$,
此時P點坐標為(8,14)或(-8,2);
③∠APB=90°時,則有PA2=PB2且PA2+PB2=AB2,
即$\left\{\begin{array}{l}{(x-6)^{2}+{y}^{2}={x}^{2}+(y-8)^{2}}\\{(x-6)^{2}+{y}^{2}+{x}^{2}+(y-8)^{2}=100}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=7}\\{y=7}\end{array}\right.$,
此時P點坐標為(-1,-1)或(7,7);
綜上可知使△PAB為等腰直角三角形的P點坐標為此時P點坐標為(13,6)或(-2,-6)或(8,14)或(-8,2)或(-1,-1)或(7,7).
點評 本題為一次函數的綜合應用,涉及函數圖象與坐標軸的交點、勾股定理、三角形的面積、角平分線的性質、等腰直角三角形的性質、分類討論思想及方程思想等知識.在(1)不注意函數圖象與坐標軸的交點的求法,在(2)中利用角平分線的性質和等積法求得OC的長是解題的關鍵,在(3)中用P點坐標分別表示出PA、PB的長,由等腰直角三角形的性質得到關于P點坐標的方程組是解題的關鍵.本題考查知識點較多,綜合性較強,計算較大,難度較大.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:填空題
 如圖,四邊形ABCD的邊AB、BC、CD、DA和⊙O分別切于L、M、N、P,且AB=10cm,CD=5cm,則四邊形ABCD周長為30cm.
如圖,四邊形ABCD的邊AB、BC、CD、DA和⊙O分別切于L、M、N、P,且AB=10cm,CD=5cm,則四邊形ABCD周長為30cm.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
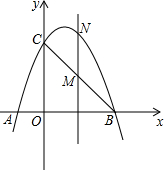 如圖,已知拋物線經過點A(-1,0),B(3,0),C(0,3)三點.
如圖,已知拋物線經過點A(-1,0),B(3,0),C(0,3)三點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (x+2y)(x-2y)=x2-4y2 | B. | x2y-xy2-1=xy(x-y)-1 | ||
| C. | a2-4ab+4b2=(a-2b)2 | D. | 2a2-2a=2a2(1-$\frac{1}{a}$) |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 單項式3ab的次數是1 | |
| B. | 單項式$\frac{2ab}{3}$的系數是2 | |
| C. | 3a-2a2b+2ab是三次三項式 | |
| D. | -4a2b,3ab,5是多項式-4a2b+3ab-5的項 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com