

分析 (1)先將a=1,k=1代入拋物線L的解析式和直線AB解析式中,進而確定出點A的坐標,再利用平移確定出拋物線L1的解析式,拋物線L1和直線AB解析式聯立確定出點B的坐標,再利用BC∥x軸,把點B的縱坐標代入拋物線L1中,確定出點D的坐標;
(2)先將k=$\frac{1}{2}$確定出直線AB的解析式,和拋物線L的解析式聯立確定出點A的坐標,再利用平移確定出拋物線L1的解析式,拋物線L1和直線AB解析式聯立確定出點B的坐標,再利用BC∥x軸,把點B的縱坐標代入拋物線L,L1中,確定出點C、E和D的坐標;
(3)直接聯立拋物線L的解析式和直線AB的解析式確定出點A的坐標,其余同(2)的方法.
解答 解:(1)當a=1,k=1時,拋物線L的解析式為:y=x2①與直線AB的解析式為y=x②,
聯立①②得,$\left\{\begin{array}{l}{y={x}^{2}}\\{y=x}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$(是原點)或$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
∴A(1,1),
∵拋物線L沿直線y=x平移得到拋物線L1,當拋物線L1過點A(1,1),
∴拋物線L1解析式為y=(x-1)2+1③,
聯立②③得,$\left\{\begin{array}{l}{y=x}\\{y=(x-1)^{2}+1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$(點A的坐標)或$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
∴B(2,2),
①∴OB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$;
②把y=2代入拋物線L1解析式y=(x-1)2+1中,得,(x-1)2+1=2,
∴x=0或x=2(點B的橫坐標),
∴D(0,2),
∴點D在y軸上;
(2)當k=$\frac{1}{2}$時,不論a取何值,$\frac{BE}{DC}$的比值是唯一確定,此值為($\sqrt{2}$-1).
理由:當k=$\frac{1}{2}$時,直線AB的解析式為y=$\frac{1}{2}$x④,
∵拋物線L的解析式為:y=ax2(a>0)⑤,
聯立④⑤得,$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=a{x}^{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$(原點)或$\left\{\begin{array}{l}{x=\frac{1}{2a}}\\{y=\frac{1}{4a}}\end{array}\right.$,
∴A($\frac{1}{2a}$,$\frac{1}{4a}$),
∴拋物線L1解析式y=a(x-$\frac{1}{2a}$)2+$\frac{1}{4a}$⑥,
聯立④⑥得,$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=a{x}^{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=\frac{1}{2a}}\\{y=\frac{1}{4a}}\end{array}\right.$(點A的坐標)或$\left\{\begin{array}{l}{x=\frac{1}{a}}\\{y=\frac{1}{2a}}\end{array}\right.$
∴B($\frac{1}{a}$,$\frac{1}{2a}$),
∵BC∥x軸,
∴把y=$\frac{1}{2a}$代入拋物線L1解析式y=a(x-$\frac{1}{2a}$)2+$\frac{1}{4a}$中,得x=0或x=$\frac{1}{a}$(點B的橫坐標),
∴D(0,$\frac{1}{2a}$),
把y=$\frac{1}{2a}$代入拋物線L解析式y=ax2中,得x=±$\frac{\sqrt{2}}{2a}$,
∴C(-$\frac{\sqrt{2}}{2a}$,$\frac{1}{2a}$),E($\frac{\sqrt{2}}{2a}$,$\frac{1}{2a}$),
∴BE=$\frac{1}{a}$-$\frac{\sqrt{2}}{2a}$=$\frac{2-\sqrt{2}}{2a}$,DC=0-(-$\frac{\sqrt{2}}{2a}$)=$\frac{\sqrt{2}}{2a}$,
∴$\frac{BE}{DC}=\frac{\frac{2-\sqrt{2}}{2a}}{\frac{\sqrt{2}}{2a}}$=$\frac{2-\sqrt{2}}{\sqrt{2}}$=$\sqrt{2}$-1.
∴當k=$\frac{1}{2}$時,不論a取何值,$\frac{BE}{DC}$的比值是唯一確定,此值為($\sqrt{2}$-1).
(3)不論a,k取何值,$\frac{BE}{DC}$的比值是唯一確定,此值為($\sqrt{2}$-1).
理由:∵拋物線L:y=ax2⑦(a>0)與直線y=kx⑧相交于點A(點A在第一象限),
∴聯立⑦⑧得,$\left\{\begin{array}{l}{y=kx}\\{y=a{x}^{2}}\end{array}\right.$,∴$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$(原點坐標)或$\left\{\begin{array}{l}{x=\frac{k}{a}}\\{y=\frac{{k}^{2}}{a}}\end{array}\right.$,
∴A($\frac{k}{a}$,$\frac{{k}^{2}}{a}$),
∵拋物線L沿直線y=kx平移得到拋物線L1,當拋物線L1過點A,
∴拋物線L1的解析式為y=a(x-$\frac{k}{a}$)2+$\frac{{k}^{2}}{a}$=ax2-2kx+$\frac{2{k}^{2}}{a}$⑨,
聯立⑧⑨得,$\left\{\begin{array}{l}{y=kx}\\{y=a{x}^{2}-2kx+\frac{2{k}^{2}}{a}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=\frac{k}{a}}\\{y=\frac{{k}^{2}}{a}}\end{array}\right.$(點A的坐標)或$\left\{\begin{array}{l}{x=\frac{2k}{a}}\\{y=\frac{2{k}^{2}}{a}}\end{array}\right.$,
∴B($\frac{2k}{a}$,$\frac{2{k}^{2}}{a}$),
∴BC∥x軸,把y=$\frac{2{k}^{2}}{a}$代入拋物線L1解析式y=ax2-2kx+$\frac{2{k}^{2}}{a}$中,得x=0或x=$\frac{2k}{a}$(點B的橫坐標),
∴D(0,$\frac{2{k}^{2}}{a}$),
把y=$\frac{2{k}^{2}}{a}$代入拋物線L解析式y=ax2中,得x=±$\frac{\sqrt{2}k}{a}$,
∴C(-$\frac{\sqrt{2}k}{a}$,$\frac{2{k}^{2}}{a}$),E($\frac{\sqrt{2}k}{a}$,$\frac{2{k}^{2}}{a}$),
∴BE=$\frac{2k}{a}$-$\frac{\sqrt{2}k}{a}$=$\frac{(2-\sqrt{2})k}{a}$,DC=0-(-$\frac{\sqrt{2}k}{a}$)=$\frac{\sqrt{2}k}{a}$,
∴$\frac{BE}{DC}=\frac{\frac{(2-\sqrt{2})k}{a}}{\frac{\sqrt{2}k}{a}}$=$\frac{2-\sqrt{2}}{\sqrt{2}}$=$\sqrt{2}$-1.
∴不論a,k取何值,$\frac{BE}{DC}$的比值是唯一確定,此值為($\sqrt{2}$-1).
點評 此題是二次函數綜合題,主要考查了待定系數法,直線和拋物線的交點坐標的確定等知識點,會解含字母系數的方程組是解本題的關鍵.


科目:初中數學 來源:2016-2017學年北京市西城區七年級上學期期末考試數學試卷(解析版) 題型:單選題
下列方程中,解為x=4的方程是( ).
A. x-1=4 B. 4x=1 C. 4x-1=3x+3 D. 2(x-1)=1
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
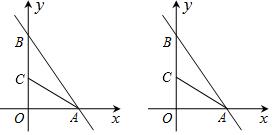
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1207×108元 | B. | 12.07×1010元 | C. | 1.207×108元 | D. | 1.207×1011元 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 7.8×103 | B. | 78.2×102 | C. | 7.82×103 | D. | 7.82×104 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com