

分析 (1)連接AD并延長,根據三角形的外角和內角關系解答;
(2)①利用(1)的結論,直接計算出∠ABX+∠ACX的度數;
②圖(3)利用(1)的結論,根據∠BDC=135°,∠BG1C=67°,計算出相等的角:∠DBG4+∠DCG4的和,再次利用(1)的結論,求出∠A的度數.
解答 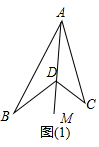 解:(1)∠BDC=∠A+∠B+∠C.理由:
解:(1)∠BDC=∠A+∠B+∠C.理由:
連接AD并延長到M.
因為∠BDM=∠BAD+∠B,∠CDM=∠CAD+∠C,
所以∠BDM+∠CDM=∠BAD+∠B+∠CAD+∠C,
即∠BDC=∠BAC+∠B+∠C.
(2)①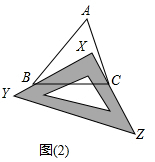 由(1)知:∠BXC=∠A+∠ABX+∠ACX,
由(1)知:∠BXC=∠A+∠ABX+∠ACX,
由于∠BXC=90°,∠A=50°
所以∠ABX+∠ACX
=∠BXC-∠A
=90°-50°
=40°.
②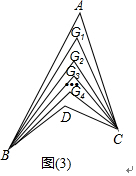 在箭頭圖G1BDC中
在箭頭圖G1BDC中
因為∠BDC=∠G1+∠G1BD+∠G1CD,
又∵∠BDC=135°,∠BG1C=67°
∵∠ABD,∠ACD的五等分線分別相交于點G1、G2、G3、G4
∴4(∠DBG4+∠DCG4)=135°-67°
∴∠DBG4+∠DCG4=17°.
∴∠ABG1+∠ACG1=17°
∵在箭頭圖G1BAC中
∵∠BG1C=∠A+∠G1BA+∠G1CA,
又∵∠BG1C=67°,
∴∠A=50°.
答:∠A的度數是50°.
點評 本題考查了外角和內角的關系以及角的計算.找出“箭頭圖”并利用“箭頭圖”間角的關系是解決本題的關鍵


科目:初中數學 來源: 題型:選擇題
| A. | 200元 | B. | 144元 | C. | 300元 | D. | 360元 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y=2x-1 | B. | y=-$\frac{1}{x}$ | C. | y=x-x2 | D. | y=$\frac{1}{{x}^{2}}$+x |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
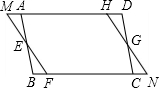 如圖四邊形ABCD、MFNH都是平行四邊形,MAHD和BFCN都在一直線上,HD=FB.
如圖四邊形ABCD、MFNH都是平行四邊形,MAHD和BFCN都在一直線上,HD=FB.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com