
分析 (1)根據等式的變化,再寫出后面兩個等式即可;
(2)通分后再開平方即可得出結論;
(3)根據等式的變化找出變化規律“$\sqrt{n+\frac{1}{n+2}}$=(n+1)$\sqrt{\frac{1}{n+2}}$(n≥1)”,此題得解.
解答 解:(1)∵$\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$;$\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$;$\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$;
∴$\sqrt{4+\frac{1}{6}}$=5$\sqrt{\frac{1}{6}}$,$\sqrt{5+\frac{1}{7}}$=6$\sqrt{\frac{1}{7}}$.
故答案為:5$\sqrt{\frac{1}{6}}$;6$\sqrt{\frac{1}{7}}$.
(2)$\sqrt{2015+\frac{1}{2017}}$=$\sqrt{\frac{2015×2017+1}{2017}}$=$\sqrt{\frac{4064256}{2017}}$=2016$\sqrt{\frac{1}{2017}}$.
(3)觀察,發現規律:$\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$;$\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$;$\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$;…,
∴$\sqrt{n+\frac{1}{n+2}}$=(n+1)$\sqrt{\frac{1}{n+2}}$(n≥1).
點評 本題考查了實數以及規律型中數字的變化類,根據等式的變化找出變化規律是解題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:選擇題
| A. | (x-1)-2(2+3x)=13 | B. | (x-1)+2(2x+3)=1 | C. | 3(x-1)+2(2+3x)=6 | D. | 3(x-1)-2(2x+3)=6 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 為檢測市場上正在銷售的酸奶質量,應該采用全面調查的方式 | |
| B. | 在連續5次的數學測試中,兩名同學的平均分相同,方差較大的同學數學成績更穩定 | |
| C. | 小強班上有3個同學都是16歲,因此小強認為他們班學生年齡的眾數是16歲 | |
| D. | 給定一組數據,則這組數據的中位數一定只有一個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
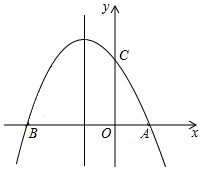 如圖,已知拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=-1,且拋物線經過A(1,0),C(0,3)兩點,與x軸相交于點B.
如圖,已知拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=-1,且拋物線經過A(1,0),C(0,3)兩點,與x軸相交于點B.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2012 | B. | 101 | C. | 100 | D. | 99 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com