
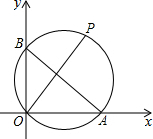 如圖,點A的坐標為A(8,0),點B在y軸正半軸上,且AB=10,點P是△AOB外接圓上一點,且∠BOP=45°,則點P的坐標為( )
如圖,點A的坐標為A(8,0),點B在y軸正半軸上,且AB=10,點P是△AOB外接圓上一點,且∠BOP=45°,則點P的坐標為( )| A. | (7,7) | B. | (7$\sqrt{2}$,7$\sqrt{2}$) | C. | (5$\sqrt{2}$,5$\sqrt{2}$) | D. | (5,5) |
分析 作PH⊥x軸于H,連結PA、PB,由A、B兩點的坐標可求出AB,由△PAB和△POH都為等腰直角三角形,得出PA=$\frac{\sqrt{2}}{2}$AB,PH=OH,設OH=t,在在Rt△PHA中,運用勾股定理求出t的值,即可得出點P的坐標.
解答 解:作PH⊥x軸于H,連結PA、PB,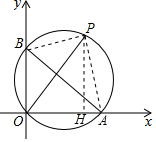
∵∠AOB=90°,
∴AB為△AOB外接圓的直徑,
∴∠BPA=90°,
∵AB=10,∠BAP=∠BOP=45°,
∴PA=5$\sqrt{2}$,
設OH=t,則PH=t,AH=8-t,
在Rt△PHA中,
∵PH2+AH2=PA2,即t2+(8-t)2=(5$\sqrt{2}$)2,
解得,t1=1(舍去),t2=7,
∴點P的坐標為(7,7),
故選:A.
點評 本題考查的是圓周角定理及等腰直角三角形的性質,根據題意作出輔助線,構造出等腰直角三角形是解答此題的關鍵.


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 李強家里搞裝修時,木工師傅想要在一塊矩形木板ABCD的中央挖去一個形狀與原矩形相同,周長是原矩形一半的小矩形(如圖),木工師傅算來算去,不知如何下手,正犯愁時,李強放學回家,見狀說:“很方便,連接AC,BD交于點O,用刻度尺分別量出AO,BO,CO,DO的中點E,F,G,H,依次連接EF,FG,GH,HE,就得到要挖去的矩形EFGH.”請你說明道理.
李強家里搞裝修時,木工師傅想要在一塊矩形木板ABCD的中央挖去一個形狀與原矩形相同,周長是原矩形一半的小矩形(如圖),木工師傅算來算去,不知如何下手,正犯愁時,李強放學回家,見狀說:“很方便,連接AC,BD交于點O,用刻度尺分別量出AO,BO,CO,DO的中點E,F,G,H,依次連接EF,FG,GH,HE,就得到要挖去的矩形EFGH.”請你說明道理.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
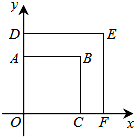 如圖,正方形OABC與正方形ODEF是位似圖形,點O為位似中心,相似比為1:$\sqrt{2}$,點B的坐標為(1,1),則點E的坐標是($\sqrt{2}$,$\sqrt{2}$).
如圖,正方形OABC與正方形ODEF是位似圖形,點O為位似中心,相似比為1:$\sqrt{2}$,點B的坐標為(1,1),則點E的坐標是($\sqrt{2}$,$\sqrt{2}$).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com