
 如圖,A為半徑18cm的⊙O上的定點,動點P從A出發,以3πcm/s的速發沿圓周按逆時針方向運動,當點P回到A地立即停止運動.
如圖,A為半徑18cm的⊙O上的定點,動點P從A出發,以3πcm/s的速發沿圓周按逆時針方向運動,當點P回到A地立即停止運動.分析 (1)當∠POA=90°時,點P運動的路程為⊙O周長的$\frac{1}{4}$或$\frac{3}{4}$,所以分兩種情況進行分析;
(2)直線BP與⊙O的位置關系是相切,根據已知可證得OP⊥BP,即直線BP與⊙O相切.
解答 解:(1)當∠POA=90°時,根據弧長公式可知點P運動的路程為⊙O周長的$\frac{1}{4}$或$\frac{3}{4}$,
設點P運動的時間為ts;
當點P運動的路程為⊙O周長的$\frac{1}{4}$時,3π•t=$\frac{1}{4}$•2π•18,
解得t=3;
當點P運動的路程為⊙O周長的$\frac{3}{4}$時,3π•t=$\frac{3}{4}$•2π•18,
解得t=9;
∴當∠POA=90°時,點P運動的時間為3s或9s.
(2)解:∵當OP⊥PB時,BP與⊙O相切,
∵AB=OA,OA=OP,
∴OB=2OP,∠OPB=90°;
∴∠B=30°;
∴∠O=60°;
∵OA=9cm,
∴$\widehat{AP}$=$\frac{60•π×9}{180}$=3π,
∴點P運動的距離為3π,
∴當t=1,有BP與⊙O相切.
點評 本題考查的是切線的性質及弧長公式,解答(2)題時要注意過圓外一點有兩條直線與圓相切,不要漏解.


科目:初中數學 來源: 題型:解答題
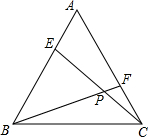 如圖,E、F分別是等邊三角形ABC的邊AB,AC上的點,且BE=AF,CE、BF交于點P.
如圖,E、F分別是等邊三角形ABC的邊AB,AC上的點,且BE=AF,CE、BF交于點P.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,反比例函數y=$\frac{k}{x}$(≠0,x>0)的圖象與直線y=3x相交于點C,過直線上點A(1,3)作AB⊥x軸于點B,交反比例函數圖象于點D,且AB=3BD.
如圖,反比例函數y=$\frac{k}{x}$(≠0,x>0)的圖象與直線y=3x相交于點C,過直線上點A(1,3)作AB⊥x軸于點B,交反比例函數圖象于點D,且AB=3BD.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增減 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com