
 已知,如圖,在⊙O中,直徑AB=4,點(diǎn)E是OA上任意一點(diǎn),過點(diǎn)E作弦CD⊥AB,點(diǎn)F是弧AB上的一點(diǎn),連接AF交CE于點(diǎn)H,連結(jié)AC,CF,BD.
已知,如圖,在⊙O中,直徑AB=4,點(diǎn)E是OA上任意一點(diǎn),過點(diǎn)E作弦CD⊥AB,點(diǎn)F是弧AB上的一點(diǎn),連接AF交CE于點(diǎn)H,連結(jié)AC,CF,BD.分析 (1)先由垂定定理得出$\widehat{AC}=\widehat{AD}$,即可得出∠ACD=∠CFA,進(jìn)而得出結(jié)論;
(2)借助(1)的結(jié)論得出AC2=AH•AF,代值即可得出結(jié)論;
(3)先由垂定定理判斷出S△AEC=S△AED,進(jìn)而得出S△AED:S△BOD=1:4,再用同高的兩三角形的面積比等于底的比得出$\frac{AE}{OB}=\frac{1}{4}$,即可求出AE.
解答 解:(1)∵CD⊥AB,
∴$\widehat{AC}=\widehat{AD}$,
∴∠ACD=∠CFA,
∵∠CAH=∠FAC,
∴△ACH∽△AFC;
(2)由(1)知,△ACH∽△AFC;
∴$\frac{AC}{AF}=\frac{AH}{AC}$,
∴AC2=AH•AF,
∵AC=$\sqrt{2}$,
∴AH•AF=2;
(3)如圖,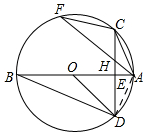 連接AD,
連接AD,
∵CD⊥AB,
∴CE=DE,
∴S△AEC=S△AED,
∵S△AEC:S△BOD=1:4,
∴S△AED:S△BOD=1:4,
∵S△AED=$\frac{1}{2}$AE•DE,S△BOD=$\frac{1}{2}$OB•DE,
∴$\frac{AE}{OB}=\frac{1}{4}$,
∵直徑AB=4,
∴OB=2,
∴AE=$\frac{1}{2}$,
∴點(diǎn)E離點(diǎn)A的距離是$\frac{1}{2}$.
點(diǎn)評 此題主要考查了垂定定理,同圓中等弧所對的圓周角相等,相似三角形的判斷和性質(zhì),同高的兩三角形的面積比等于底的比,解本題的關(guān)鍵判斷出△ACH∽△AFC和用同高的兩三角形的面積比等于底的比,是一道中等難度的中考常考題.


 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
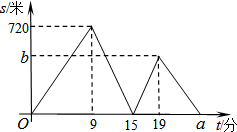 小寧、小波從學(xué)校出發(fā)到青少年宮參加書法比賽,小寧步行一段時間后,小波騎自行車沿相同路線行進(jìn),兩人均勻速前行.他們的路程差s(米)與小寧出發(fā)時間t(分)之間的函數(shù)關(guān)系如圖所示.下列說法:①小波先到達(dá)青少年宮;②小波的速度是小寧速度的2.5倍;③a=25;④b=460.其中正確的是( )
小寧、小波從學(xué)校出發(fā)到青少年宮參加書法比賽,小寧步行一段時間后,小波騎自行車沿相同路線行進(jìn),兩人均勻速前行.他們的路程差s(米)與小寧出發(fā)時間t(分)之間的函數(shù)關(guān)系如圖所示.下列說法:①小波先到達(dá)青少年宮;②小波的速度是小寧速度的2.5倍;③a=25;④b=460.其中正確的是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,點(diǎn)M是直線y=2x+3在第二象限上的動點(diǎn),過點(diǎn)M作MN垂直x軸于點(diǎn)N,在y軸的正半軸上求點(diǎn)P,使△MNP為等腰直角三角形,請寫出符合條件的點(diǎn)P的坐標(biāo)(0,0)、(0,1)或(0,$\frac{3}{4}$).
如圖,點(diǎn)M是直線y=2x+3在第二象限上的動點(diǎn),過點(diǎn)M作MN垂直x軸于點(diǎn)N,在y軸的正半軸上求點(diǎn)P,使△MNP為等腰直角三角形,請寫出符合條件的點(diǎn)P的坐標(biāo)(0,0)、(0,1)或(0,$\frac{3}{4}$).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 對于有理數(shù)a,b,定義一種新運(yùn)算“⊙”,規(guī)定a⊙b=|a+b|+|a-b|.
對于有理數(shù)a,b,定義一種新運(yùn)算“⊙”,規(guī)定a⊙b=|a+b|+|a-b|.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 二次函數(shù)y=$\frac{2}{3}$x2的圖象如圖所示,點(diǎn)A0位于坐標(biāo)原點(diǎn),點(diǎn)A1,A2,A3,…,A2017在y軸的正半軸上,點(diǎn)B1,B2,B3,…,B2017在二次函數(shù)y=$\frac{2}{3}$x2位于第一象限的圖象上,△A0B1A1,△A1B2A2,△A2B3A3,…,△A2016B2017A2017都為等邊三角形,則等邊△A2016B2017A2017的高為$\frac{2017\sqrt{3}}{2}$,.
二次函數(shù)y=$\frac{2}{3}$x2的圖象如圖所示,點(diǎn)A0位于坐標(biāo)原點(diǎn),點(diǎn)A1,A2,A3,…,A2017在y軸的正半軸上,點(diǎn)B1,B2,B3,…,B2017在二次函數(shù)y=$\frac{2}{3}$x2位于第一象限的圖象上,△A0B1A1,△A1B2A2,△A2B3A3,…,△A2016B2017A2017都為等邊三角形,則等邊△A2016B2017A2017的高為$\frac{2017\sqrt{3}}{2}$,.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com