Question

8．如圖，點M是直線y=2x+3在第二象限上的動點，過點M作MN垂直x軸于點N，在y軸的正半軸上求點P，使△MNP為等腰直角三角形，請寫出符合條件的點P的坐標（0，0）、（0，1）或（0，$\frac{3}{4}$）．

Answer 1

分析 設點M的坐標為（m，2m+3），由點M在第二象限且在直線y=2x+3上，利用一次函數圖象上點的坐標特征即可得出m的取值范圍，分∠MNP=90°、∠NMP=90°以及∠MPN=90°三種情況考慮，利用等腰直角三角形的性質找出點M的坐標，將其代入一次函數解析式中求出m值，由此即可得出點P的坐標．

解答 解：設點M的坐標為（m，2m+3），
令y=2x+3＞0，解得：x＞-$\frac{3}{2}$，
∴-$\frac{3}{2}$＜x＜0．
當∠MNP=90°時，MN=ON，
∴點M的坐標為（m，-m），
∵點M在直線y=2x+3上，
∴-m=2m+3，
解得：m=-1，
∴點P的坐標為（0，0）；
當∠NMP=90°時，MN=PM，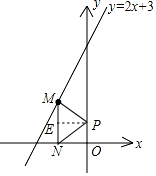
∴點M的坐標為（m，-m），
∵點M在直線y=2x+3上，
∴-m=2m+3，
解得：m=-1，
∴點P的坐標為（0，1）；
當∠MPN=90°時，過點P作PE⊥MN于點E，
∵△MNP為等腰直角三角形，
∴MN=2PE，
∴點M的坐標為（m，-2m），
∵點M在直線y=2x+3上，
∴-2m=2m+3，
解得：m=-$\frac{3}{4}$，
∴點P的坐標為（0，$\frac{3}{4}$）．
綜上可知：符合條件的點P的坐標為（0，0）、（0，1）或（0，$\frac{3}{4}$）．

點評 本題考查了一次函數圖象上點的坐標特征以及等腰直角三角形的性質，分∠MNP=90°、∠NMP=90°以及∠MPN=90°三種情況考慮是解題的關鍵．