
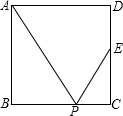
 如圖所示,四邊形ABCD是正方形,E是CD的中點,P是BC邊上的一點,下列條件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中點;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )
如圖所示,四邊形ABCD是正方形,E是CD的中點,P是BC邊上的一點,下列條件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中點;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
分析 利用相似三角形的判定定理,以及正方形的性質逐項判斷即可.
解答 解:∵四邊形ABCD為正方形,
∴AB=BC=CD,∠B=∠C=90°,
∵E為CD中點,
∴CD=2CE,即AB=BC=2CE,
①當∠APB=∠EPC時,結合∠B=∠C,可推出△ABP∽△ECP;
②當∠APE=∠APB≠60°時,則有∠APB≠∠EPC,所以不能推出△ABP∽△ECP;
③當P是BC中點時,則有BC=2PC,可知PC=CE,則△PCE為等腰直角三角形,而BP≠AB,即△ABP不是等腰直角三角形,故不能推出△ABP∽△ECP;④當BP:BC=2:3時,則有BP:PC=2:1,且AB:CE=2:1,結合∠B=∠C,可推出△ABP∽△ECP相似;
故選B.
點評 本題考查了相似三角形的判定定理:(1)兩角對應相等的兩個三角形相似.(2)兩邊對應成比例且夾角相等的兩個三角形相似.(3)三邊對應成比例的兩個三角形相似.(4)如果一個直角三角形的斜邊和一條直角邊與另一個直角三角形的斜邊和一條直角邊對應成比例,那么這兩個直角三角形相似.也考查了正方形的性質.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
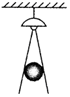 如圖,在一間黑屋子里用一盞白熾燈照一個球,球在地面上的陰影的形狀是一個圓,當把球向遠離燈的位置移動時,圓形陰影面積的大小的變化情況是變小.
如圖,在一間黑屋子里用一盞白熾燈照一個球,球在地面上的陰影的形狀是一個圓,當把球向遠離燈的位置移動時,圓形陰影面積的大小的變化情況是變小.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | 5 | C. | 1或5 | D. | 無法計算 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
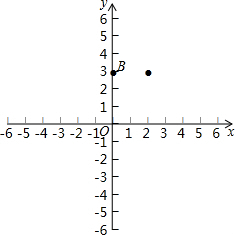 已知拋物線y=ax2+bx+c的頂點為A,經過點B(0,3)和點(2,3),與x軸交于C,D兩點,(點C在點D的左側),且OD=OB.
已知拋物線y=ax2+bx+c的頂點為A,經過點B(0,3)和點(2,3),與x軸交于C,D兩點,(點C在點D的左側),且OD=OB.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com