
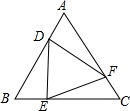
 如圖,等邊△ABC中,點D,E,F分別同時從點A,B,C出發,以相同的速度在AB,BC,CA上運動,連結DE,EF,DF.
如圖,等邊△ABC中,點D,E,F分別同時從點A,B,C出發,以相同的速度在AB,BC,CA上運動,連結DE,EF,DF.分析 (1)根據等邊三角形的性質得出∠A=∠B=∠C=60°,AB=BC=CA,AD=BE=CF,進一步證得BD=EC=AF,即可證得△ADF≌△BED≌△CFE,根據全等三角形的性質得出DE=EF=FD,即可證得△DEF是等邊三角形;
(2)①根據等邊三角形得:DE、EF、DF是中位線,由中位線定理得兩三角形相似,其相似比為1:2,則面積比為1:4;
②分兩種情況:當∠EFC=90°時,如圖3,∠FEC=30°,當∠CEF=90°時,如圖4,由△ABC和△DEF是等邊三角形,得出△DEF∽△ABC,再根據相似三角形的性質即可得出結論.
解答 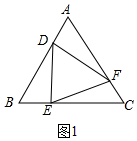 (1)證明:∵△ABC是等邊三角形,
(1)證明:∵△ABC是等邊三角形,
∴∠A=∠B=∠C=60°,AB=BC=CA,
∵AD=BE=CF,
∴BD=EC=AF,
在△ADF、△BED和△CFE中
$\left\{\begin{array}{l}{AD=BE=CF}\\{∠A=∠B=∠C}\\{BD=CE=AF}\end{array}\right.$
∴△ADF≌△BED≌△CFE,
∴DE=EF=FD,
∴△DEF是等邊三角形;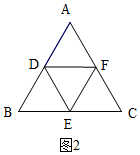
解:(2)有,
①如圖2,∵△CEF是等邊三角形,
∴EC=FC=EF,
∵AD=BE=CF,
∴D、E、F分別是三邊的中點,
∴$\frac{DF}{BC}=\frac{DE}{AC}=\frac{EF}{AB}=\frac{1}{2}$,
∴△DEF∽△BCA,
∴$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=$\frac{1}{4}$;
②∵△ABC和△DEF是等邊三角形,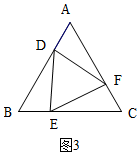
∴△DEF∽△ABC,
當∠EFC=90°時,∠FEC=30°,
∵∠DEF=60°,
∴DE⊥BC,
∴∠BDE=30°,
∴BE=$\frac{1}{2}$BD,即BE=$\frac{1}{3}$BC,CE=$\frac{2}{3}$BC,
∵EF=EC•sin60°=$\frac{2}{3}BC$$•\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{3}BC$,
∴$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=($\frac{EF}{BC}$)2=($\frac{\sqrt{3}}{3}$)2=$\frac{1}{3}$.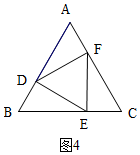
當∠CEF=90°時,如圖4,同理可得:$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=($\frac{EF}{BC}$)2=($\frac{\sqrt{3}}{3}$)2=$\frac{1}{3}$.
點評 本題是三角形的綜合題,考查的是等邊三角形的性質和判定、三角形中位線定理、三角形相似的性質和判定以及動點運動問題,熟知三個動點同時同速度時,路程相等,并知道等邊三角形的三個內角都相等,且都等于60°.


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案科目:初中數學 來源: 題型:選擇題
 如圖所示,在一塊長為22m,寬為17m的矩形地面上,要修建同樣寬的兩條互相垂直的道路(兩條道路各與矩形的一條邊平行),若剩余部分種上草坪,使草坪的面積為300m2,則所修道路的寬度為( )m.
如圖所示,在一塊長為22m,寬為17m的矩形地面上,要修建同樣寬的兩條互相垂直的道路(兩條道路各與矩形的一條邊平行),若剩余部分種上草坪,使草坪的面積為300m2,則所修道路的寬度為( )m.| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
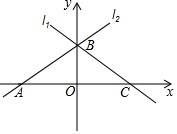 如圖,直線l1與直線l2關于y軸對稱,已知直線l1的函數表達式為y=-$\frac{4}{3}$x+b,點B 坐標為(0,3),則點A坐標為(-$\frac{9}{4}$,0).
如圖,直線l1與直線l2關于y軸對稱,已知直線l1的函數表達式為y=-$\frac{4}{3}$x+b,點B 坐標為(0,3),則點A坐標為(-$\frac{9}{4}$,0).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
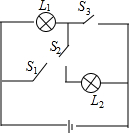 如圖所示電路,任意閉合兩個開關,能使燈L2亮起來的概率是( )
如圖所示電路,任意閉合兩個開關,能使燈L2亮起來的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com