
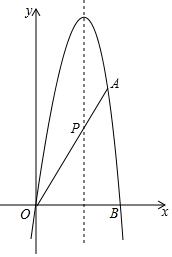
 拋物線y=-$\sqrt{3}$x2+bx+c經(jīng)過點O(0,0),A(4,4$\sqrt{3}$),與x軸的另一交點為點B,且拋物線的對稱軸與線段OA交于點P.
拋物線y=-$\sqrt{3}$x2+bx+c經(jīng)過點O(0,0),A(4,4$\sqrt{3}$),與x軸的另一交點為點B,且拋物線的對稱軸與線段OA交于點P.分析 (1)把O(0,0),A(4,4$\sqrt{3}$)的坐標代入y=-$\sqrt{3}$x2+bx+c,轉化為解方程組即可.
(2)先求出直線OA的解析式,點B坐標,拋物線的對稱軸即可解決問題.
(3)①如圖1中,點O關于直線BQ的對稱點為點C,當點C恰好在直線l上時,首先證明四邊形BOQC是菱形,設Q(m,$\frac{5\sqrt{3}}{2}$),根據(jù)OQ=OB=5,可得方程m2+($\frac{5\sqrt{3}}{2}$)2=52,解方程即可解決問題.
②如圖2中,由題意點D在以B為圓心5為半徑的⊙B上運動,當A、D、B共線時,線段AD最小,設OD與BQ交于點H.先求出D、H兩點坐標,再求出直線BH的解析式即可解決問題.
解答 解:(1)把O(0,0),A(4,4$\sqrt{3}$)的坐標代入y=-$\sqrt{3}$x2+bx+c,
得$\left\{\begin{array}{l}{c=0}\\{-16\sqrt{3}+4b+c=4\sqrt{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=5\sqrt{3}}\\{c=0}\end{array}\right.$,
∴拋物線的解析式為y=-$\sqrt{3}$x2+5$\sqrt{3}$x.
(2)由題意B(5,0),A(4,4$\sqrt{3}$),
∴直線OA的解析式為y=$\sqrt{3}$x,AB=$\sqrt{{1}^{2}+(4\sqrt{3})^{2}}$=7,
∵拋物線的對稱軸x=$\frac{5}{2}$,
∴P($\frac{5}{2}$,$\frac{5\sqrt{3}}{2}$).
(3)①如圖1中,點O關于直線BQ的對稱點為點C,當點C恰好在直線l上時,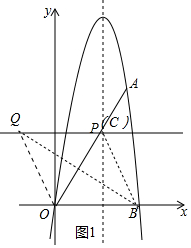
∵QC∥OB,
∴∠CQB=∠QBO=∠QBC,
∴CQ=BC=OB=5,
∴四邊形BOQC是平行四邊形,
∵BO=BC,
∴四邊形BOQC是菱形,
設Q(m,$\frac{5\sqrt{3}}{2}$),
∴OQ=OB=5,
∴m2+($\frac{5\sqrt{3}}{2}$)2=52,
∴m=±$\frac{5}{2}$,
∴點Q坐標為(-$\frac{5}{2}$,$\frac{5\sqrt{3}}{2}$)或($\frac{5}{2}$,$\frac{5\sqrt{3}}{2}$)
②如圖2中,由題意點D在以B為圓心5為半徑的⊙B上運動,當A、D、B共線時,線段AD最小,設OD與BQ交于點H.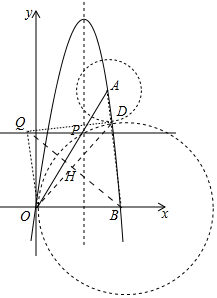
∵AB=7,BD=5,
∴AD=2,D($\frac{30}{7}$,$\frac{20\sqrt{3}}{7}$),
∵OH=HD,
∴H($\frac{15}{7}$,$\frac{10\sqrt{3}}{7}$),
∴直線BH的解析式為y=-$\frac{\sqrt{3}}{2}$x+$\frac{5\sqrt{3}}{2}$,
當y=$\frac{5\sqrt{3}}{2}$時,x=0,
∴Q(0,$\frac{5\sqrt{3}}{2}$).
點評 本題考查二次函數(shù)綜合題、一次函數(shù)的應用、平行四邊形的判定和性質、菱形的判定和性質、勾股定理、圓等知識,解題的關鍵是靈活運用所學知識,學會用方程的思想思考問題,學會構建一次函數(shù),利用方程組求交點坐標,屬于中考壓軸題.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | (0,-2) | B. | (0,2) | C. | (2,0) | D. | (-2,0) |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,△ABC的頂點坐標分別為A(4,5),B(2,3),C(5,1).
如圖,△ABC的頂點坐標分別為A(4,5),B(2,3),C(5,1).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
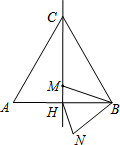 如圖,邊長為4a的等邊三角形ABC中,M是高CH所在直線上的一個動點,連結MB,將線段BM繞點B逆時針旋轉60°得到BN,連接HN.則在點M運動過程中,線段HN長度的最小值是( )
如圖,邊長為4a的等邊三角形ABC中,M是高CH所在直線上的一個動點,連結MB,將線段BM繞點B逆時針旋轉60°得到BN,連接HN.則在點M運動過程中,線段HN長度的最小值是( )| A. | 2a | B. | a | C. | $\frac{1}{2}$a | D. | $\frac{1}{3}$a |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com