
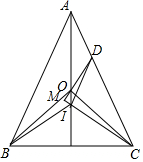
 △ABC中,AB=AC,O、I分別是其外心、內(nèi)心,點(diǎn)D在AC上,且DI∥AB,DO的延長(zhǎng)線交CI的延長(zhǎng)線于M.求證:DM⊥CM.
△ABC中,AB=AC,O、I分別是其外心、內(nèi)心,點(diǎn)D在AC上,且DI∥AB,DO的延長(zhǎng)線交CI的延長(zhǎng)線于M.求證:DM⊥CM. 分析 先用平行線的性質(zhì)和三角形的外角的性質(zhì)得出∠AID=∠CAM,進(jìn)而得出點(diǎn)O,I,C,D四點(diǎn)共圓,再用直角三角形的兩銳角互余即可得出結(jié)論.
解答 證明: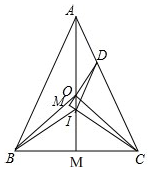
∵O是△ABC的外心,AB=AC,
∴AM⊥BC,
∴∠CAM=$\frac{1}{2}$∠BAC,
∵DI∥AB,
∴∠IDC=∠BAC=2∠CAM,
∵∠IDC=∠CAM+∠ADO(三角形的一個(gè)外角等于與它不相鄰的兩內(nèi)角的和),
∴∠AID=∠CAM,
∵O是△ABC的外心,
∴OA=OC,
∴∠ACO=∠CAM,
∴∠AID=∠ACO,
∴點(diǎn)O,I,C,D四點(diǎn)共圓,
∴∠ODI=∠OCI,
∵I是△ABC的內(nèi)心,
∴∠ACI=∠ICM,
∵OA=OC,
∴∠COM=2∠CAM,
在Rt△COM中,∠COM+∠OCM=90°,
∴∠ODC+∠ACI
=∠ODI+∠IDC+∠ACI
=∠OCI+2∠CAM+∠ACM
=∠COM+∠OCM
=90°,
∴∠CMD=90°,
∴DM⊥CM.
點(diǎn)評(píng) 此題是三角形五心,主要考查了三角形內(nèi)心與外心的性質(zhì)、圓周角定理、四點(diǎn)共圓的判定方法和等腰三角形的性質(zhì);判斷點(diǎn)O,I,C,D四點(diǎn)共圓是解本題的關(guān)鍵.


 學(xué)期復(fù)習(xí)一本通學(xué)習(xí)總動(dòng)員期末加暑假延邊人民出版社系列答案
學(xué)期復(fù)習(xí)一本通學(xué)習(xí)總動(dòng)員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
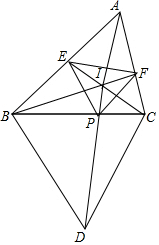 如圖,△ABC中,∠A=60°,以BC為邊往外作等邊△BCD,作∠B,∠C的角平分線分別交AC,AB于點(diǎn)F,E,若BE,CF交于點(diǎn)I,連接ID交BC于點(diǎn)P,求證:△EFP為等邊三角形.
如圖,△ABC中,∠A=60°,以BC為邊往外作等邊△BCD,作∠B,∠C的角平分線分別交AC,AB于點(diǎn)F,E,若BE,CF交于點(diǎn)I,連接ID交BC于點(diǎn)P,求證:△EFP為等邊三角形.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
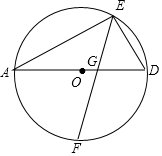 以AD為直徑作⊙O,F(xiàn)是半圓弧$\widehat{AD}$上中點(diǎn),E是半圓弧$\widehat{AD}$上一點(diǎn),EA=8,ED=6,連接EF交AD于點(diǎn)G,求tan∠AGF的值.
以AD為直徑作⊙O,F(xiàn)是半圓弧$\widehat{AD}$上中點(diǎn),E是半圓弧$\widehat{AD}$上一點(diǎn),EA=8,ED=6,連接EF交AD于點(diǎn)G,求tan∠AGF的值.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
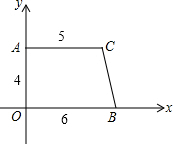 如圖,在直角梯形AOBC中,AC平行于OB,且OB=6,AC=5,OA=4,
如圖,在直角梯形AOBC中,AC平行于OB,且OB=6,AC=5,OA=4,查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
 如圖,它是一個(gè)數(shù)值轉(zhuǎn)換機(jī),若輸入的a值為$\sqrt{2}$,則輸出的結(jié)果應(yīng)為-$\frac{2\sqrt{3}}{3}$.
如圖,它是一個(gè)數(shù)值轉(zhuǎn)換機(jī),若輸入的a值為$\sqrt{2}$,則輸出的結(jié)果應(yīng)為-$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
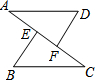 如圖,在△AFD和△CEB中,點(diǎn)A、E、F、C在同一條直線上,有下列四個(gè)判斷:①AD=CB;②AE=CF;③∠B=∠D;④∠A=∠C.請(qǐng)以其中三個(gè)為已知條件,剩下一個(gè)作為結(jié)論,編一道數(shù)學(xué)題(用序號(hào)???⇒?的形式寫出),并寫出證明過(guò)程.
如圖,在△AFD和△CEB中,點(diǎn)A、E、F、C在同一條直線上,有下列四個(gè)判斷:①AD=CB;②AE=CF;③∠B=∠D;④∠A=∠C.請(qǐng)以其中三個(gè)為已知條件,剩下一個(gè)作為結(jié)論,編一道數(shù)學(xué)題(用序號(hào)???⇒?的形式寫出),并寫出證明過(guò)程.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com