
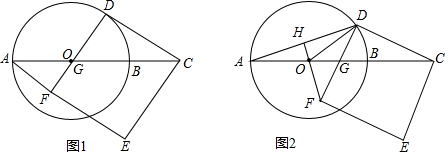
分析 (1)在Rt△ODC中,求出∠ACD的值即可解決問題.
(2)①設OG=GB=a,則OB=BC=OD=2a,可知OD2=OG•OC=4a2,推出$\frac{OD}{OG}$=$\frac{OC}{OD}$,由∠DOG=∠COD,即可證明△DOG∽△COD.
②連接BD,作GM⊥AD于M,GN⊥DB于N.只要證明∠BDG=∠CDB=∠ADG,由GM⊥AD,GN⊥DB,推出GM=GN,可知S△ADG:S△DGB=$\frac{1}{2}$AD•GM:$\frac{1}{2}$•DB•GN=AD+DB=AG:GB=3:1,推出tan∠DAC=$\frac{DB}{AD}$=$\frac{1}{3}$即可.
解答 (1)解:如圖1中,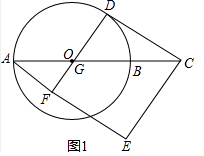
∵四邊形EFDC是正方形,
∴∠ODC=90°,
∵OB=BC=OD,
∴OC=2OD,
∴sin∠ACD=$\frac{OD}{OC}$=$\frac{1}{2}$,
∴∠ACD=30°.
(2)解:如圖2中,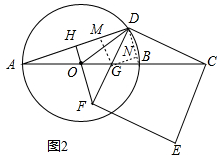
①證明:設OG=GB=a,則OB=BC=OD=2a,
∴OD2=OG•OC=4a2,
∴$\frac{OD}{OG}$=$\frac{OC}{OD}$,∵∠DOG=∠COD,
∴△DOG∽△COD.
②連接BD,作GM⊥AD于M,GN⊥DB于N.
∵AB是直徑,
∴∠ADB=∠GDC=90°,
∴∠ADG=∠CDB,
∵△DOG∽△COD,
∴∠ODG=∠DCB,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠ODG+∠BDG=∠BDC+∠DCB,
∴∠BDG=∠CDB=∠ADG,
∵GM⊥AD,GN⊥DB,
∴GM=GN,
∵S△ADG:S△DGB=$\frac{1}{2}$AD•GM:$\frac{1}{2}$•DB•GN=AD+DB=AG:GB=3:1,
∴$\frac{DB}{AD}$=$\frac{1}{3}$,
∴tan∠DAC=$\frac{DB}{AD}$=$\frac{1}{3}$.
點評 本題考查相似三角形的判定和性質、正方形的性質、解直角三角形、圓周角定理、勾股定理等知識,解題的關鍵是學會利用參數解決問題,本題體現了數形結合的數學思想,學會添加常用輔助線,掌握用面積法證明線段之間的關系,屬于中考壓軸題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
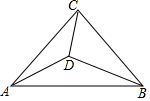 如圖,在等腰直角△ABC中,∠ACB=90°,點D為三角形內一點,且∠ACD=∠DAB=∠DBC.
如圖,在等腰直角△ABC中,∠ACB=90°,點D為三角形內一點,且∠ACD=∠DAB=∠DBC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
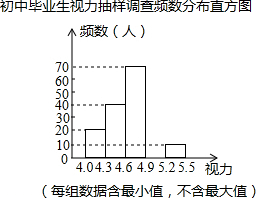 某區對即將參加中考的5000名初中畢業生進行了一次視力抽樣調查,繪制出頻數分布表和不完整的頻數分布直方圖,請根據圖表信息回答下列問題:
某區對即將參加中考的5000名初中畢業生進行了一次視力抽樣調查,繪制出頻數分布表和不完整的頻數分布直方圖,請根據圖表信息回答下列問題:| 視力 | 頻數(人) | 頻率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com