
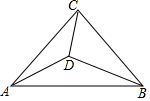
 如圖,在等腰直角△ABC中,∠ACB=90°,點D為三角形內一點,且∠ACD=∠DAB=∠DBC.
如圖,在等腰直角△ABC中,∠ACB=90°,點D為三角形內一點,且∠ACD=∠DAB=∠DBC.分析 (1)只要證明∠CDA=135°,∠ADB=135°即可解決問題.
(2)根據兩角對應相等兩三角形相似即可判定.
(3)由△DCA∽△DAB,推出$\frac{DC}{DA}$=$\frac{DA}{DB}$=$\frac{AC}{BA}$=$\frac{1}{\sqrt{2}}$,又CD=1,推出AD=$\sqrt{2}$,DB=2.根據BC=$\sqrt{C{D}^{2}+B{D}^{2}}$,求出BC,再在Rt△ABC中,求出AB即可解決問題.
解答 (1)解:∵△ABC為等腰直角三角形,
∴∠CAB=45°.
又∵∠ACD=∠DAB,
∴∠ACD+∠CAD=∠DAB+∠CAD=∠CAB=45°,
∴∠CDA=135°
同理可得∠ADB=135°
∴∠CDB=360°-∠CDA-∠ADB=360°-135°-135°=90°.
(2)證明:∵∠CDA=∠ADB,∠ACD=∠DAB,
∴△DCA∽△DAB
(3)解:∵△DCA∽△DAB,
∴$\frac{DC}{DA}$=$\frac{DA}{DB}$=$\frac{AC}{BA}$=$\frac{1}{\sqrt{2}}$,
又∵CD=1,
∴AD=$\sqrt{2}$,DB=2.
又∵∠CDB=90°,
∴BC=$\sqrt{C{D}^{2}+B{D}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
在Rt△ABC中,∵AC=BC=$\sqrt{5}$,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{10}$.
點評 本題考查相似三角形的判定和性質、等腰直角三角形的性質、勾股定理等知識,解題的關鍵是靈活運用所學知識解決問題,本題的突破點是發現∠CDB=90°,屬于中考常考題型.


科目:初中數學 來源: 題型:選擇題
 如圖,直線l:y=$\frac{\sqrt{3}}{3}$x,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2;…按此作法繼續下去,則點A2015的坐標為( )
如圖,直線l:y=$\frac{\sqrt{3}}{3}$x,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2;…按此作法繼續下去,則點A2015的坐標為( )| A. | (0,42015) | B. | (0,42014) | C. | (0,32015) | D. | (0,32014) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
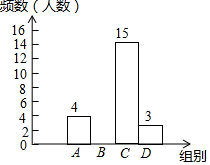 為豐富學生的校園生活,某校舉行“與愛同行”朗誦比賽,賽后整理參賽同學的成績,繪制成如下不完整的統計圖表,請根據圖表中的信息解答下列問題.
為豐富學生的校園生活,某校舉行“與愛同行”朗誦比賽,賽后整理參賽同學的成績,繪制成如下不完整的統計圖表,請根據圖表中的信息解答下列問題. | 組別 | 成績x(分) | 頻數(人數) |
| A | 8.0≤x<8.5 | a |
| B | 8.5≤x<9.0 | 8 |
| C | 9.0≤x<9.5 | 15 |
| D | 9.5≤x<10 | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
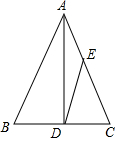 如圖,已知AD是等腰△ABC底邊BC上的高,sinB=$\frac{4}{5}$,點E在AC上,且AE:EC=2:3,則tan∠ADE=( )
如圖,已知AD是等腰△ABC底邊BC上的高,sinB=$\frac{4}{5}$,點E在AC上,且AE:EC=2:3,則tan∠ADE=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com