
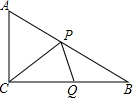
 如圖,Rt△ABC中,∠ACB=90°,CA=3cm,CB=4cm,設點P、Q為AB、CB上動點,它們分別從A、C同時出發向B點勻速移動,移動速度都為1cm/秒,移動時間為t秒(0≤t≤4),在整個移動過程中,
如圖,Rt△ABC中,∠ACB=90°,CA=3cm,CB=4cm,設點P、Q為AB、CB上動點,它們分別從A、C同時出發向B點勻速移動,移動速度都為1cm/秒,移動時間為t秒(0≤t≤4),在整個移動過程中,分析 (1)過P作MP⊥AC與M,作PN⊥CB于N,易得AB=5cm,PM∥BC,利用△APM∽△ACB的相似比可表示出MP=$\frac{4}{5}$t,AM=$\frac{3}{5}$t,則CM=3-$\frac{3}{5}$t,在Rt△PCM中利用勾股定理得到PC2=PM2+MC2=($\frac{4}{5}$t)2+(3-$\frac{3}{5}$t)2=t2-$\frac{18}{5}$t+9;又Rt△CPN∽Rt△CQP,得到CP2=CN•CQ=$\frac{4}{5}$t•t,由此可得到關于t的一元二次方程,解方程即可得到t的值;
(2)分三種情況:①CP=CQ時;②CP=PQ時;③CQ=PQ時;進行討論即可求解.
解答 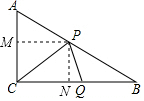 解:(1)過P作MP⊥AC與M,作PN⊥CB于N,如圖,AP=CQ=t,
解:(1)過P作MP⊥AC與M,作PN⊥CB于N,如圖,AP=CQ=t,
∵∠ACB=90°,CA=3cm,CB=4cm,
∴AB=5cm,PM∥BC,
∴△APM∽△ACB,
∴MP:BC=AM:AC=AP:AB,
∴MP=$\frac{4}{5}$t,AM=$\frac{3}{5}$t,
∴CM=3-$\frac{3}{5}$t,
在Rt△PCM中,PC2=PM2+MC2=($\frac{4}{5}$t)2+(3-$\frac{3}{5}$t)2=t2-$\frac{18}{5}$t+9,
又∵CN=PM=$\frac{4}{5}$t,
∵∠CPQ=90°,
∴Rt△CPN∽Rt△CQP,
∴CP:CQ=CN:CP,即CP2=CN•CQ,
∴t2-$\frac{18}{5}$t+9=($\frac{4}{5}$t)•t,整理得:t2-18t+45=0,
∴t1=3(t2=15舍去),
∴當∠CPQ=90°時,t的值為3;
(2)①CP=CQ時,t2-$\frac{18}{5}$t+9=t2,t=2.5;
②CP=PQ時,CN=$\frac{1}{2}$CQ,$\frac{4}{5}$t=$\frac{1}{2}$t,t=0(舍);
③CQ=PQ時,t2=(3-$\frac{3}{5}$t)2+(t-$\frac{4}{5}$t)2,
t1=2$\sqrt{6}$-3,t2=2$\sqrt{6}$+3(舍).
綜上:t=2.5或t=2$\sqrt{6}$-3時,△CPQ是等腰三角形.
點評 本題考查了三角形相似的判定與性質:有兩組角對應相等的兩個三角形相似;相似三角形對應邊的比相等.也考查了等腰三角形的判定與性質以及勾股定理.注意分類思想的應用.


 培優三好生系列答案
培優三好生系列答案 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:初中數學 來源: 題型:填空題
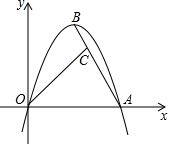 已知二次函數y=ax2+2$\sqrt{3}$x(a<0)的圖象與x軸交于A(6,0),頂點為B,C為線段AB上一點,BC=2,D為x軸上一動點.若BD=OC,則D的坐標為D(2,0)或(4,0).
已知二次函數y=ax2+2$\sqrt{3}$x(a<0)的圖象與x軸交于A(6,0),頂點為B,C為線段AB上一點,BC=2,D為x軸上一動點.若BD=OC,則D的坐標為D(2,0)或(4,0).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 20元 | B. | 19元 | C. | 18元 | D. | 17元 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
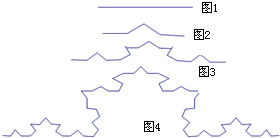 若圖1中的線段長為1,將此線段三等分,并以中間的一段為邊作等邊三角形,然后去掉這一段,得到圖2稱第1次操作,再將圖2中的每一段類似變形,得到圖3即第2次操作,按上述方法繼續得到圖4為第3次操作,則第4次操作后折線的總長度為$\frac{64}{27}$.
若圖1中的線段長為1,將此線段三等分,并以中間的一段為邊作等邊三角形,然后去掉這一段,得到圖2稱第1次操作,再將圖2中的每一段類似變形,得到圖3即第2次操作,按上述方法繼續得到圖4為第3次操作,則第4次操作后折線的總長度為$\frac{64}{27}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
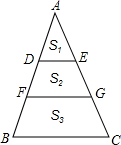 如圖,△ABC中,DE∥FG∥BC.
如圖,△ABC中,DE∥FG∥BC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
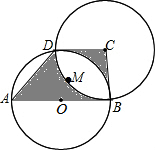 如圖,AB為圓O的直徑,點D在圓O上,在梯形ABCD中:
如圖,AB為圓O的直徑,點D在圓O上,在梯形ABCD中:查看答案和解析>>
科目:初中數學 來源: 題型:填空題
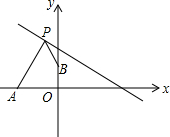 如圖,點A的坐標為(-2,0),點B的坐標為(0,1),點P在直線y=-$\frac{1}{2}$x+2上運動,當線段|AP-BP|最長時,點P的坐標是(1,$\frac{3}{2}$).
如圖,點A的坐標為(-2,0),點B的坐標為(0,1),點P在直線y=-$\frac{1}{2}$x+2上運動,當線段|AP-BP|最長時,點P的坐標是(1,$\frac{3}{2}$).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com