
| A. | 6 | B. | 8 | C. | 9 | D. | 13 |
分析 由b+c=a3-a、bc=a2知ab+bc+ca=a2+a(a3-a)=a4,將b、c看作方程x2-(b+c)x+bc=0的兩根,即方程x2+(a-a3)x+a2=0有兩個實數根,可得△=(a-a3)2-4a2≥0,即a6-2a4-3a2≥0,由a2≠0可得a2-3≥0,即a2≥3,繼而可得答案.
解答 解:∵a,b,c均為非零實數,a+b+c=abc=a3,
∴b+c=a3-a,bc=a2,
∴ab+bc+ca=a2+a(a3-a)=a4,
∵b、c是方程x2-(b+c)x+bc=0的兩根,
∴方程x2+(a-a3)x+a2=0有兩個實數根,
則△=(a-a3)2-4a2≥0,即a6-2a4-3a2≥0
∵a2≠0,
∴a4-2a2-3≥0,即(a2-3)(a2+1)≥0,
由a2≥1可得a2-3≥0,即a2≥3,
∴ab+bc+ca=a2+a(a3-a)=a4≥9,
即ab+bc+ca的最小值為9,
故選:C.
點評 本題主要考查一元二次方程的判別式、因式分解的應用,根據題意將待求代數式用同一個字母表示且構建一個以b、c為根的方程是解題的關鍵.


 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案科目:初中數學 來源: 題型:選擇題
| A. | 144元 | B. | 150元 | C. | 153元 | D. | 167元 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,河岸邊有座塔AB,小敏在河對岸C處測得塔頂A的仰角為30°,向塔前進20米到達D處,又測得塔頂A的仰角為45°,請根據上述數據計算水塔的高.
如圖,河岸邊有座塔AB,小敏在河對岸C處測得塔頂A的仰角為30°,向塔前進20米到達D處,又測得塔頂A的仰角為45°,請根據上述數據計算水塔的高.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,AB為半圓O的直徑,C為半圓上一點,∠AOC=60°,點P在AB的延長線上,且PB=BO=3cm.連接PC交半圓于點D,過P作PE⊥PA交AD的延長線于點E,求PE長.
如圖,AB為半圓O的直徑,C為半圓上一點,∠AOC=60°,點P在AB的延長線上,且PB=BO=3cm.連接PC交半圓于點D,過P作PE⊥PA交AD的延長線于點E,求PE長.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
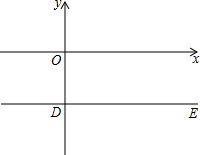 已知:直線l:y=2x+2b與過點D(0,-2)平行于x軸的直線DE交于B點,與x軸交于點A.
已知:直線l:y=2x+2b與過點D(0,-2)平行于x軸的直線DE交于B點,與x軸交于點A.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,△ABC為等邊三角形,D,E兩點分別在AB,AC邊上,DB=AE,BE,CD相交于點F,BH⊥CD于點H,若EF=1,CD=9,求HF的長.
如圖,△ABC為等邊三角形,D,E兩點分別在AB,AC邊上,DB=AE,BE,CD相交于點F,BH⊥CD于點H,若EF=1,CD=9,求HF的長.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com