
分析 把x=4,y=3代入$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$得$\left\{\begin{array}{l}{4{a}_{1}+3{b}_{1}={c}_{1}}\\{4{a}_{2}+4{b}_{2}={c}_{2}}\end{array}\right.$,把第一個(gè)方程組的兩個(gè)方程的兩邊都乘以6得到24(a2-a1)+18(b2-b1)=6(c2-c1),把第二個(gè)方程組的兩個(gè)方程相減得到3(a2-a1)(x-1)+2(b2-b1)(y-1)=6(c2-c1于是得到方程3(x-1)=24,2(y-1)=18,求得結(jié)論.
解答 解:把x=4,y=3代入$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$得$\left\{\begin{array}{l}{4{a}_{1}+3{b}_{1}={c}_{1}}\\{4{a}_{2}+4{b}_{2}={c}_{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{24{a}_{1}+18{a}_{1}=6{c}_{1}}\\{24{a}_{2}+18{b}_{2}=6{c}_{2}}\end{array}\right.$,
∴24(a2-a1)+18(b2-b1)=6(c2-c1),
∵方程組$\left\{\begin{array}{l}{3{a}_{1}(x-1)+2{b}_{1}(y+1)=6{c}_{1}}\\{3{a}_{2}(x-1)+2{b}_{2}(y+1)=6{c}_{2}}\end{array}\right.$,
∴3(a2-a1)(x-1)+2(b2-b1)(y-1)=6(c2-c1),
∴3(a2-a1)(x-1)+2(b2-b1)(y-1)=24(a2-a1)+18(b2-b1),
∴3(x-1)=24,2(y-1)=18,
解得:x=9,y=10,
∴第二個(gè)方程組的解是$\left\{\begin{array}{l}{x=9}\\{y=10}\end{array}\right.$.
點(diǎn)評(píng) 本題考查了二元一次方程組的解,解二元一次方程組,能夠準(zhǔn)確的解二元一次方程組是解題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 3個(gè) | B. | 2個(gè) | C. | 1個(gè) | D. | 0個(gè) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 已知:線段a,直線1及l(fā)外一點(diǎn)A.
已知:線段a,直線1及l(fā)外一點(diǎn)A.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 已知坐標(biāo)平面內(nèi)的三個(gè)點(diǎn)A(1,3),B(3,1),O(0,0),
已知坐標(biāo)平面內(nèi)的三個(gè)點(diǎn)A(1,3),B(3,1),O(0,0),查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 15號(hào) | B. | 16號(hào) | C. | 17號(hào) | D. | 18號(hào) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
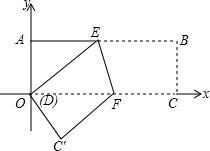 如圖,在直角坐標(biāo)系中,長(zhǎng)方形紙片ABCD的邊AB∥CO,點(diǎn)B坐標(biāo)為(9,3),若把圖形按如圖所示折疊,使B、D兩點(diǎn)重合,折痕為EF.
如圖,在直角坐標(biāo)系中,長(zhǎng)方形紙片ABCD的邊AB∥CO,點(diǎn)B坐標(biāo)為(9,3),若把圖形按如圖所示折疊,使B、D兩點(diǎn)重合,折痕為EF.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com