
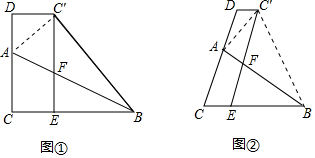
分析 【探究推廣】根據C′D∥CE,C′E∥CD,得到四邊形DCEC′是平行四邊形,根據平行四邊形的性質得到CD=EC′,根據折疊的性質得到AC=AC′,∠CAB=∠C′AB,根據平行線的性質得到∠CAF=∠AFC′,等量代換得到∠C′AF=∠C′FA,根據等腰三角形的判定定理得到AC′=C′F,于是得到結論;
【結論應用】:由【探究推廣】知,AD=EF,根據相似三角形的性質即可得到結論.
解答  解:【探究推廣】:AD=EF,
解:【探究推廣】:AD=EF,
理由:∵C′D∥CE,C′E∥CD,
∴四邊形DCEC′是平行四邊形,
∴CD=EC′,
∵將△ACB翻折至△AC′B的位置,
∴AC=AC′,∠CAB=∠C′AB,
∵CD∥C′E,
∴∠CAF=∠AFC′,
∴∠C′AF=∠C′FA,
∴AC′=C′F,
∴C′F=AC,
∴CD-AC=C′E-C′F,即AD=EF;
【結論應用】:由【探究推廣】知,AD=EF,
∵AD=2,
∴EF=2,
∵EF∥AC,
∴△EFB∽△CBA,
∴$\frac{{S}_{△BEF}}{{S}_{△BCA}}$=($\frac{EF}{AC}$)2=($\frac{2}{3}$)2=$\frac{4}{9}$,
∵S△BEF=4,
∴△ACB的面積=9.
點評 本題考查了翻折變換-軸對稱問題,平行四邊形的判定和性質,平行線的性質,相似三角形的判定和性質,正確的理解題意是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在△ABC中,∠BAC=90°,AB=AC=3,點D在BC上且BD=2CD,E,F分別在AB,AC上運動且始終保持∠EDF=45°,設BE=x,CF=y,則y與x之間的函數關系用圖象表示為:( )
如圖,在△ABC中,∠BAC=90°,AB=AC=3,點D在BC上且BD=2CD,E,F分別在AB,AC上運動且始終保持∠EDF=45°,設BE=x,CF=y,則y與x之間的函數關系用圖象表示為:( )| A. | 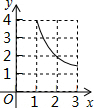 | B. | 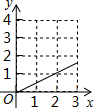 | C. | 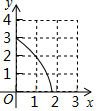 | D. | 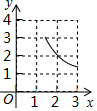 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
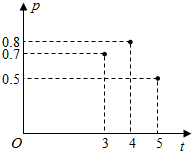 加工爆米花時,爆開且不糊的粒數占加工總粒數的百分比稱為“可食用率”,在特定條件下,可食用率p與加工時間t(單位:分鐘)滿足函數關系p=at2+bt-2(a,b是常數),如圖記錄了三次實驗的數據,根據上述函數模型和實驗數據,可得到最佳加工時間為( )
加工爆米花時,爆開且不糊的粒數占加工總粒數的百分比稱為“可食用率”,在特定條件下,可食用率p與加工時間t(單位:分鐘)滿足函數關系p=at2+bt-2(a,b是常數),如圖記錄了三次實驗的數據,根據上述函數模型和實驗數據,可得到最佳加工時間為( )| A. | 3.75分鐘 | B. | 4.00分鐘 | C. | 4.15分鐘 | D. | 4.25分鐘 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一點,將Rt△ABC沿CD折疊,使B點落在AC邊上的B′處,則∠CDB′等于( )
如圖,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一點,將Rt△ABC沿CD折疊,使B點落在AC邊上的B′處,則∠CDB′等于( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
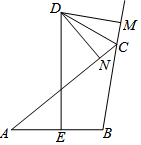 已知,如圖,DE為△ABC的邊AB的垂直平分線,CD為△ABC的外角平分線,與DE交于D,DM⊥BC于M,DN⊥AC于N,若CM=1,BC=3,求AN的長.
已知,如圖,DE為△ABC的邊AB的垂直平分線,CD為△ABC的外角平分線,與DE交于D,DM⊥BC于M,DN⊥AC于N,若CM=1,BC=3,求AN的長.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com