16.
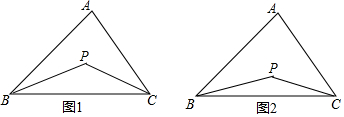
【提出問題】已知如圖1,P是∠ABC、∠ACB的角平分線的交點,你能找到∠P、∠A的關系嗎?
【分析問題】在解決這個問題時,某小組同學是這樣做的:
先賦予∠A幾個特殊值:
當∠A=80°時,計算出∠P=130°;
當∠A=40°時,計算出∠P=110°;
當∠A=100°時,計算出∠P=140°;
…由以上特例猜想∠P與∠A的關系為:∠P=90°+$\frac{1}{2}$∠A.再證明這一結論:
證明:∵點P是∠ABC、∠ACB的角平分線的交點.
∴∠PBC=$\frac{1}{2}$∠ABC;∠PCB=$\frac{1}{2}$∠ACB
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)
又∵∠A+(∠ABC+∠ACB)=180°
∴∠ABC+∠ACB=180°-∠A
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)
=$\frac{1}{2}$(180°-∠A)
∴∠P=180°-(∠PBC+∠PCB)
=180°-$\frac{1}{2}$(180°-∠A)
=90°+$\frac{1}{2}$∠A
【解決問題】請運用以上解決問題的“思想方法”解決下面的幾個問題:
(1)如圖2,若點P時∠ABC、∠ACB的三等分線的交點,即∠PBC=$\frac{1}{3}$∠ABC,∠PCB=$\frac{1}{3}$∠ACB,猜測∠P與∠A的關系為∠P=$\frac{1}{3}$∠A+$\frac{2}{3}$×180°,證明你的結論.
(2)若點P時∠ABC、∠ACB的四等分線的交點,即∠PBC=$\frac{1}{4}$∠ABC,∠PCB=$\frac{1}{4}$∠ACB,則∠P與∠A的關系為∠P=$\frac{1}{4}$∠A+$\frac{3}{4}$×180°.(直接寫出答案,不需要證明)
(3)若點P時∠ABC、∠ACB的n等分線的交點,即∠PBC=$\frac{1}{n}$∠ABC,∠PCB=$\frac{1}{n}$∠ACB,則∠P與∠A的關系為$\frac{n-1}{n}$•180°+$\frac{1}{n}$∠A.(直接寫出答案,不需要證明)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 【提出問題】已知如圖1,P是∠ABC、∠ACB的角平分線的交點,你能找到∠P、∠A的關系嗎?
【提出問題】已知如圖1,P是∠ABC、∠ACB的角平分線的交點,你能找到∠P、∠A的關系嗎? 如圖,點A、B、C、D為圓O的四等分點,動點P從圓心O出發,沿線段OC-弧CD-線段DO的路線作勻速運動.設運動時間為t秒,∠APB的度數為y度,則下列圖象中表示y與t的函數關系最恰當的是( )
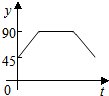
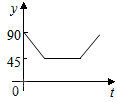
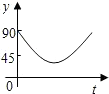
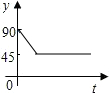
如圖,點A、B、C、D為圓O的四等分點,動點P從圓心O出發,沿線段OC-弧CD-線段DO的路線作勻速運動.設運動時間為t秒,∠APB的度數為y度,則下列圖象中表示y與t的函數關系最恰當的是( )