
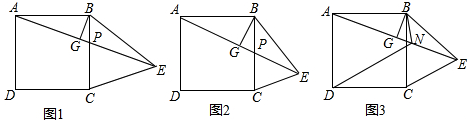
分析 (1)先根據(jù)線段垂直平分線的性質(zhì),求得AB=BE=2$\sqrt{2}$,再根據(jù)勾股定理,求得Rt△ABP中,AP=3,最后根據(jù)△ABP的面積,求得BG的長(zhǎng);
(2)先過C作CH⊥AE于H,判定△BGP≌△CHP(AAS),根據(jù)全等三角形對(duì)應(yīng)邊相等以及等腰三角形的性質(zhì),得出△CEH為等腰直角三角形,進(jìn)而得到CE=$\sqrt{2}$CH=$\sqrt{2}$BG;
(3)先過點(diǎn)D作DH⊥AE于H先判定△BGN為等腰直角三角形,得出BG=GN,BN=$\sqrt{2}$GN,再判定△ADH≌△BAG(AAS),得出AH=BG=GN,DH=AG,進(jìn)而得到HN=HG+GN=HG+AH=AG,DH=HN,再根據(jù)△DHN為等腰直角三角形,得出DN=$\sqrt{2}$HN=$\sqrt{2}$AG,最后得到BN+DN=$\sqrt{2}$GN+$\sqrt{2}$AG=$\sqrt{2}$AN.
解答 (1)解:∵AG=GE,BG⊥AP,
∴AB=BE=2$\sqrt{2}$,
∵正方形ABCD中,∠ABP=90°,AB=2$\sqrt{2}$,PB=1,
∴Rt△ABP中,AP=$\sqrt{(2\sqrt{2})^{2}+{1}^{2}}$=3,
∵△ABP的面積=$\frac{1}{2}$×AP×BG=$\frac{1}{2}$×AB×BP,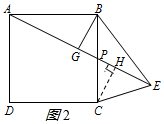
∴BG=$\frac{2\sqrt{2}}{3}$;
(2)證明:如圖2,過C作CH⊥AE于H,
∵BG⊥AE,
∴∠BGP=∠CHP=90°,
∵P為BC的中點(diǎn),
∴BP=CP,
在△BGP和△CHP中,$\left\{\begin{array}{l}{∠BGP=∠CHP}&{\;}\\{∠BPG=∠CPH}&{\;}\\{BP=CP}&{\;}\end{array}\right.$,
∴△BGP≌△CHP(AAS),
∴BG=CH,∠GBP=∠PCH,
∵AB=BE,
∴∠BAE=∠BEA,
∵∠ABC=∠ABG+∠GBP=90°,∠ABG+∠BAG=90°,
∴∠GBP=∠BAG,
∴∠PCH=∠BEP,
∵AB=BC,AB=BE,
∴BC=BE,
∴∠BCE=∠BEC,
∴∠HCE=∠HEC,
∴CH=EH,
∵∠CHE=90°,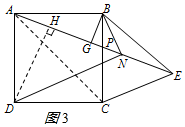
∴CE=$\sqrt{2}$CH,即CE=$\sqrt{2}$BG;
(3)解:如圖3,過點(diǎn)D作DH⊥AE于H
∵BN平分∠CBE,
∴∠CBN=∠EBN,
由(2)可知∠GBP=∠BEP,
∵BG⊥AE,
∴∠GBP+∠PBN=45°,即∠GBN=45°=∠GNB,
∴BG=GN,BN=$\sqrt{2}$GN,
∵DH⊥AP,∠DAB=90°,
∴∠DAH+∠ADH=∠DAH+∠BAD=90°,
∴∠ADH=∠BAG,
在△ADH和△BAG中,$\left\{\begin{array}{l}{∠ADH=∠BAG}&{\;}\\{∠AHD=∠AGB}&{\;}\\{AD=BA}&{\;}\end{array}\right.$,
∴△ADH≌△BAG(AAS),
∴AH=BG=GN,DH=AG,
∴HN=HG+GN=HG+AH=AG,
∴DH=HN,
∵∠DHN=90°,
∴DN=$\sqrt{2}$HN=$\sqrt{2}$AG,
∴BN+DN=$\sqrt{2}$GN+$\sqrt{2}$AG=$\sqrt{2}$AN.
點(diǎn)評(píng) 本題是四邊形綜合題目,考查了正方形的性質(zhì),線段垂直平分線的性質(zhì),等腰直角三角形的性質(zhì),全等三角形的判定和性質(zhì),勾股定理的綜合運(yùn)用等知識(shí);本題綜合性強(qiáng),有一定難度,證明三角形全等是解決問題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
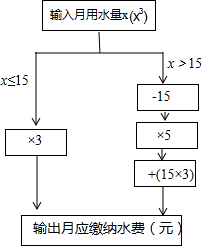 小明根據(jù)市自來水公司的居民用水收費(fèi)標(biāo)準(zhǔn),制定了如圖所示的水費(fèi)計(jì)算數(shù)值轉(zhuǎn)換機(jī)示意圖,根據(jù)數(shù)值轉(zhuǎn)換機(jī)程序,小明輸入他家這個(gè)月的用水量,結(jié)果顯示應(yīng)繳水費(fèi)70元,那么小明家這個(gè)月的用水量為20m3.
小明根據(jù)市自來水公司的居民用水收費(fèi)標(biāo)準(zhǔn),制定了如圖所示的水費(fèi)計(jì)算數(shù)值轉(zhuǎn)換機(jī)示意圖,根據(jù)數(shù)值轉(zhuǎn)換機(jī)程序,小明輸入他家這個(gè)月的用水量,結(jié)果顯示應(yīng)繳水費(fèi)70元,那么小明家這個(gè)月的用水量為20m3.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
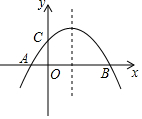 如圖,已知拋物線y=-$\frac{1}{m}$(x+2)(x-m)(m>0)與x軸相交于點(diǎn)A、B,與y軸相交于點(diǎn)C,且點(diǎn)A在點(diǎn)B的左側(cè).
如圖,已知拋物線y=-$\frac{1}{m}$(x+2)(x-m)(m>0)與x軸相交于點(diǎn)A、B,與y軸相交于點(diǎn)C,且點(diǎn)A在點(diǎn)B的左側(cè).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
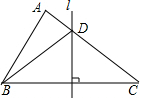 如圖,△ABC中,AB+AC=6cm,BC的垂直平分線l與AC相交于點(diǎn)D,則△ABD的周長(zhǎng)為( )
如圖,△ABC中,AB+AC=6cm,BC的垂直平分線l與AC相交于點(diǎn)D,則△ABD的周長(zhǎng)為( )| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,將△ABC繞頂點(diǎn)C旋轉(zhuǎn)得到△A′B′C,且點(diǎn)B剛好落在A′B′上,若∠A=25°,∠BCA′=45°,則∠ABC等于( )
如圖,將△ABC繞頂點(diǎn)C旋轉(zhuǎn)得到△A′B′C,且點(diǎn)B剛好落在A′B′上,若∠A=25°,∠BCA′=45°,則∠ABC等于( )| A. | 40° | B. | 55° | C. | 65° | D. | 70° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 將長(zhǎng)方形紙片ABCD的∠C沿著GF折疊(點(diǎn)F在BC上,不與B,C重合),使點(diǎn)C落在長(zhǎng)方形內(nèi)部點(diǎn)E處,若FH平分∠EFB,則∠GFH等于( )
將長(zhǎng)方形紙片ABCD的∠C沿著GF折疊(點(diǎn)F在BC上,不與B,C重合),使點(diǎn)C落在長(zhǎng)方形內(nèi)部點(diǎn)E處,若FH平分∠EFB,則∠GFH等于( )| A. | 80° | B. | 85° | C. | 90° | D. | 95° |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com