
分析 由于該函數沒有說明是二次函數,故a-1應分兩種情況進行討論.
解答 解:(1)當a-1=0,即a=1時,函數為一次函數y=-2x+1,符合題意.
(2)當a-1≠0,即a≠1時,函數為二次函數
①圖象與x軸只有一個交點.此時△=0
∴4-4a(a-1)=0,
解得:a=$\frac{1±\sqrt{5}}{2}$,
此時拋物線與x軸、y軸各有一個交點,符合題意,
②圖象過原點(0,0)代入y=(a-1)x2-2x+a,得a=0,
∴綜上所述,a=1或a=0或$a=\frac{{1+\sqrt{5}}}{2}或{a_{\;}}=\frac{{1-\sqrt{5}}}{2}$
點評 本題考查二次函數與x軸的交點問題,涉及一元二次方程的解法,一次函數圖象的性質.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
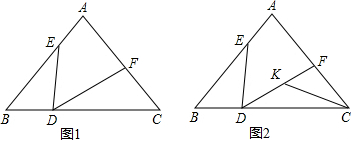
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
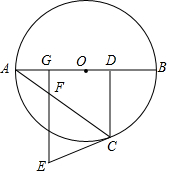 如圖,AB是圓O之間,C是圓O上一點,過C作CD⊥AB于D,EC與圓O相切于C且CE=CD.
如圖,AB是圓O之間,C是圓O上一點,過C作CD⊥AB于D,EC與圓O相切于C且CE=CD.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在△ABC中,∠CAB=67°,將△ABC在平面內繞點A旋轉到△AB′C′的位置,使CC′∥AB,則旋轉角的度數為( )
如圖,在△ABC中,∠CAB=67°,將△ABC在平面內繞點A旋轉到△AB′C′的位置,使CC′∥AB,則旋轉角的度數為( )| A. | 46° | B. | 50° | C. | 65° | D. | 67° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
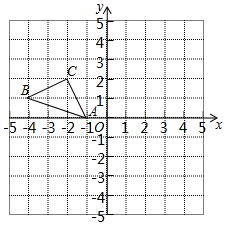 正方形網格中(網格中的每個小正方形邊長是1),△ABC的頂點均在格點上,請在所給的直角坐標系中解答下列問題:
正方形網格中(網格中的每個小正方形邊長是1),△ABC的頂點均在格點上,請在所給的直角坐標系中解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
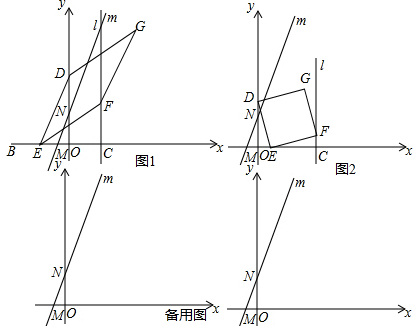
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 9cm | B. | 5cm | C. | 6cm或5cm | D. | 5cm或9cm |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角頂點C為旋轉中心,將△ABC旋轉到△A′B′C的位置,其中A′、B′分別是A、B的對應點,且點B在斜邊A′B′上,直角邊CA′交AB于D,則旋轉角等于( )
如圖,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角頂點C為旋轉中心,將△ABC旋轉到△A′B′C的位置,其中A′、B′分別是A、B的對應點,且點B在斜邊A′B′上,直角邊CA′交AB于D,則旋轉角等于( )| A. | 70° | B. | 80° | C. | 60° | D. | 50° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com