Question

16．如圖，A（0，6），B（-6，0），點C、D同時從點O、A出發以每秒1個單位的速度分別沿著x軸正半軸和射線AO方向運動，同時點E從點B出發，以每秒2個單位沿著射線BO運動，過點C的直線l⊥x軸，點F是直線l在x軸上方的一點，且EF=ED，以DE和EF為鄰邊作菱形DEFG；當點C和點E重合時各點同時停止運動；直線m：y=2x+2交x軸于點M，交y軸于點N；設運動時間為t．

（1）如圖1直接寫出點M和點N的坐標并用t的代數式表示CE和OD的長度．
M（-1，0），N（0，2），CE=6-t，OD=6-t．．
（2）如圖2，當點E在線段OC之間時，證明：菱形DEFG為正方形．
（3）在整個運動過程中，
①當t的值為多少時，四邊形DEFG有一個頂點落在直線m上；
②記點D關于直線m的對稱點為點D′，當點D′恰好落在直線l上時，直接寫出t的值是$\frac{16}{9}$．

Answer 1

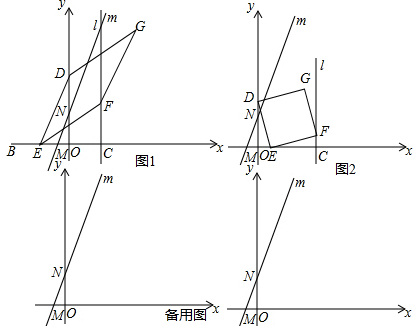
分析 （1）求出直線y=2x+2與坐標軸的交點，可得M、N點坐標，由題意OE=t，AD=t，BE=2t，可以推出CE、OD的長．
（2）根據一個角是90°的菱形是正方形，只要證明∠DEF=90°即可．
（3）①分四種情形分別討論即可．②如圖5中，設DD′交直線m于F，作FG⊥OA于G．由△DFG∽△FNG∽△MNO，得$\frac{DG}{FG}$=$\frac{FG}{GN}$=$\frac{OM}{ON}$=$\frac{1}{2}$，推出DG=$\frac{1}{4}$t，GN=t，
根據GN=AN-AD-DG，列出方程即可解決問題．

解答 解：（1）∵y=2x+2交x軸于點M，交y軸于點N，
∴M（-1，0），N（0，2），
由題意，OE=t，AD=t，BE=2t，
∴EC=OB+OC-BE=6+t-2t=6-t，OD=OA-AD=6-t，
故答案為（-1，0），（0，2），6-t，6-t，

（2）證明：點E在線段OC之間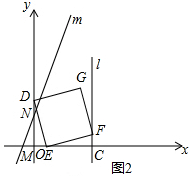

∵CE=6-t=OD，EF=ED，∠DOE=∠ECF=90°．
∴△DOE≌△ECF
∴∠DEO=∠EFC
∴∠DEO+∠CEF=∠EFC+∠CEF=90°，
∴∠DEF=90°
∴菱形DEFG是正方形．

（3）①當點D落在直線m上；即點D與點N重合，
可得6-t=2
∴t=4．
當點E落在直線m上；即點E與點M重合，
可得2t=5
∴t=2.5．

當點F落在直線m上；如圖3，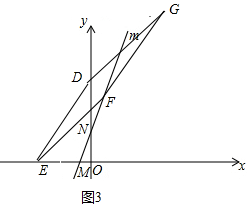

由△DOE≌△FCE
可得CF=OE=6-2t
把F （ t，6-2t ）代入y=2x+2
6-2t=2t+2
∴t=1．
當點G落在直線m上；如圖4，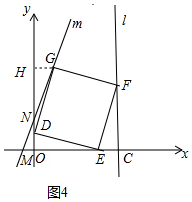

過G作GH⊥x軸于點H
容易證明△DOE≌△GHD；
∴GH=OD=6-t，HD=OE=2t-6
∴OH=HD+OD=t
把G （6-t，t ）代入y=2x+2
t=2（6-t）+2∴t=$\frac{14}{3}$．
∴當t取4，2.5，1，$\frac{14}{3}$時，四邊形DEFG有一個頂點落在直線m上

②如圖5中，設DD′交直線m于F，作FG⊥OA于G．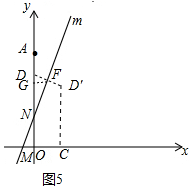

由題意，D關于直線m的對稱點為點D′，當點D′恰好落在直線l上，
∴FG=$\frac{t}{2}$，AD=t，
由△DFG∽△FNG∽△MNO，
∴$\frac{DG}{FG}$=$\frac{FG}{GN}$=$\frac{OM}{ON}$=$\frac{1}{2}$，
∴DG=$\frac{1}{4}$t，GN=t，
∵GN=AN-AD-DG，
∴t=4-t-$\frac{1}{4}$t，
∴t=$\frac{16}{9}$．
∴t=$\frac{16}{9}$時，D關于直線m的對稱點為點D′，當點D′恰好落在直線l上．

點評 本題考查一次函數綜合題、全等三角形 的判定和性質，相似三角形的判定和性質正方形的判定和性質，解題的關鍵是靈活運用所學知識，學會用分類討論的思想思考問題，學會添加常用輔助線，構造相似三角形解決問題，屬于中考壓軸題．